Understanding fractions and decimals is essential in mathematics, and converting between the two can be a crucial skill. The decimal 0.8 is a straightforward number to work with, but what is it in fraction form simplified?
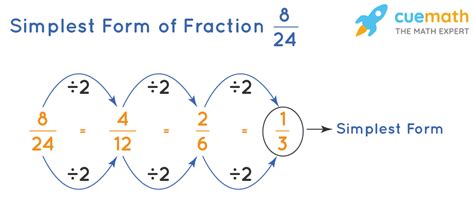
To convert 0.8 to a fraction, we can follow a simple step-by-step process. First, we recognize that 0.8 is eight tenths, since the decimal point moves one place to the right when converting from a decimal to a fraction. So, 0.8 is equal to 8/10.
However, 8/10 is not in its simplest form. To simplify this fraction, we need to find the greatest common divisor (GCD) of 8 and 10. The GCD of 8 and 10 is 2. To simplify the fraction, we divide both the numerator (8) and the denominator (10) by the GCD (2).
Simplifying the fraction, we get 8 ÷ 2 / 10 ÷ 2 = 4/5. So, 0.8 in fraction form simplified is 4/5.

Why Is Simplifying Fractions Important?
Simplifying fractions is a fundamental concept in mathematics, and it has numerous applications in various fields. Here are a few reasons why simplifying fractions is important:
Easy Comparisons
Simplifying fractions makes it easier to compare them. When fractions are in their simplest form, it's easier to determine which fraction is larger or smaller.
Accurate Calculations
Simplifying fractions ensures that calculations are accurate. When fractions are in their simplest form, calculations such as addition, subtraction, multiplication, and division become more manageable.
Reducing Errors
Simplifying fractions reduces the likelihood of errors. When fractions are not in their simplest form, it's easier to make mistakes, especially when performing calculations.
Real-World Applications of Simplifying Fractions
Simplifying fractions has numerous real-world applications. Here are a few examples:
Cooking and Recipes
When following a recipe, it's essential to simplify fractions to ensure accurate measurements. For instance, if a recipe calls for 3/4 cup of flour, it's crucial to understand that it's equivalent to 0.75 cups.
Shopping and Sales
When shopping during sales, it's essential to simplify fractions to compare prices. For instance, if a product is on sale for 1/3 off, it's crucial to understand that it's equivalent to 33.33% off.
Science and Engineering
Simplifying fractions is crucial in science and engineering, where precise calculations are essential. For instance, in physics, simplifying fractions helps calculate complex formulas and equations.
Common Mistakes When Simplifying Fractions
When simplifying fractions, it's essential to avoid common mistakes. Here are a few:
Not Finding the GCD
One of the most common mistakes is not finding the greatest common divisor (GCD) of the numerator and the denominator.
Not Simplifying Properly
Another common mistake is not simplifying the fraction properly. For instance, 8/10 can be simplified to 4/5, but 4/10 is not the correct simplified form.
Conclusion
In conclusion, 0.8 in fraction form simplified is 4/5. Simplifying fractions is an essential skill in mathematics, and it has numerous applications in various fields. By understanding how to simplify fractions, you can make accurate calculations, reduce errors, and apply mathematical concepts to real-world problems.
If you have any questions or need further clarification on simplifying fractions, please leave a comment below. Share this article with your friends and family to help them understand the importance of simplifying fractions.
What is the simplified form of 0.8 as a fraction?
+The simplified form of 0.8 as a fraction is 4/5.
Why is simplifying fractions important?
+Simplifying fractions is important because it makes calculations easier, reduces errors, and allows for accurate comparisons.
What is the greatest common divisor (GCD) of 8 and 10?
+The greatest common divisor (GCD) of 8 and 10 is 2.