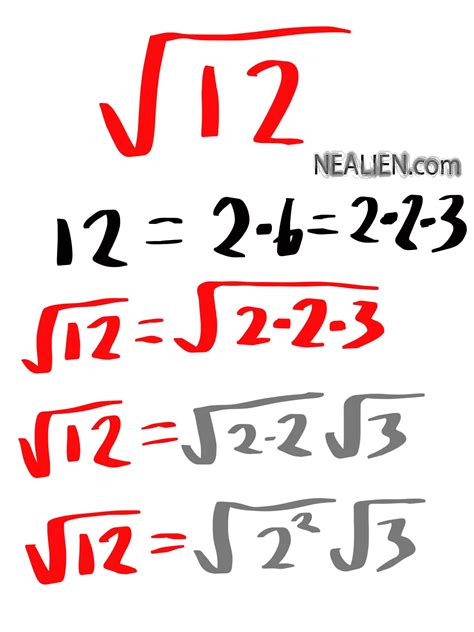Simplify The Square Root Of 208 In Radical Form

Quick Links :

To simplify the square root of 208 in radical form, we need to find the largest perfect square that divides 208.

208 = 2 × 2 × 2 × 2 × 13

We can take the square root of the perfect square factors:

√208 = √(2 × 2 × 2 × 2 × 13) = √(16 × 13) = 4√13

Therefore, the simplified form of the square root of 208 in radical form is 4√13.

Prime Factorization and Simplification

When simplifying square roots, it's essential to understand prime factorization. Prime factorization is the process of breaking down a number into its prime factors. In the case of 208, we can break it down into its prime factors:

208 = 2 × 2 × 2 × 2 × 13

By taking the square root of the perfect square factors, we can simplify the expression. This process helps us to identify the largest perfect square that divides the original number.

Radicals and Radical Form

A radical is a symbol used to represent the square root of a number. In the simplified form of √208, we have:

4√13

This expression represents the square root of 208 in radical form. The radical sign (√) indicates that we are taking the square root of the number inside the radical.

Key Concepts and Terms

• Square root: A mathematical operation that finds the number that, when multiplied by itself, gives a specified value.
• Radical: A symbol used to represent the square root of a number.
• Radical form: A way of expressing a number using a radical symbol.
• Perfect square: A number that can be expressed as the square of an integer.
• Prime factorization: The process of breaking down a number into its prime factors.

By understanding these concepts and applying them to the problem, we can simplify the square root of 208 in radical form to 4√13.

Applications and Real-World Examples

Simplifying square roots in radical form has various applications in mathematics and real-world problems. Some examples include:

• Geometry: Simplifying square roots is essential in geometry to calculate distances, lengths, and areas.
• Algebra: Radical form is used in algebra to solve equations and manipulate expressions.
• Physics: Square roots are used in physics to calculate distances, velocities, and energies.

By mastering the skill of simplifying square roots in radical form, we can tackle a wide range of mathematical and real-world problems.

Common Mistakes and Misconceptions

When simplifying square roots in radical form, some common mistakes and misconceptions include:

• Not identifying perfect squares: Failing to identify perfect squares can lead to incorrect simplification.
• Not using prime factorization: Not using prime factorization can make it difficult to simplify square roots.
• Not applying the rules of radicals: Not applying the rules of radicals can lead to incorrect simplification.

By being aware of these common mistakes and misconceptions, we can improve our skills in simplifying square roots in radical form.

Conclusion

In conclusion, simplifying the square root of 208 in radical form requires a good understanding of prime factorization, radicals, and radical form. By applying these concepts and avoiding common mistakes, we can simplify the expression to 4√13.

Take Action

Take a moment to practice simplifying square roots in radical form. Try simplifying the square root of 256 or 324. By practicing, you'll become more confident and proficient in your ability to simplify square roots.

FAQ