Vertex Form Of Parabolas Calculator Tool

Quick Links :

The study of parabolas is an essential part of mathematics, particularly in algebra and geometry. A parabola is defined as the set of all points that are equidistant to the focus F and the directrix. In this article, we will focus on the vertex form of parabolas and explore how to use a calculator tool to find the vertex of a parabola.

Understanding Parabolas

A parabola is a quadratic curve that opens upwards or downwards. It has a single vertex, which is the lowest or highest point on the curve, depending on the direction of the opening. The standard form of a parabola is given by the equation y = ax^2 + bx + c, where a, b, and c are constants.

Vertex Form of Parabolas

The vertex form of a parabola is given by the equation y = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. This form is useful for finding the vertex of a parabola, as it provides the coordinates of the vertex directly.

Benefits of Vertex Form

The vertex form of parabolas has several benefits, including:

• It provides the coordinates of the vertex directly, making it easier to find the vertex of a parabola.
• It allows for easier graphing of the parabola, as the vertex form provides the coordinates of the vertex and the direction of the opening.
• It is useful for solving problems that involve the vertex of a parabola, such as finding the maximum or minimum value of a quadratic function.

Using a Calculator Tool to Find the Vertex of a Parabola

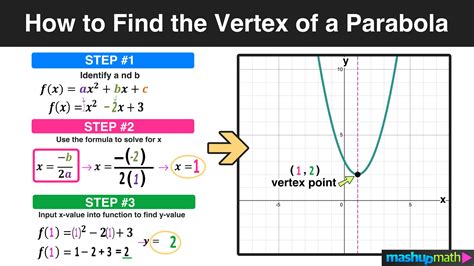
A calculator tool can be used to find the vertex of a parabola by entering the values of a, b, and c into the calculator and using the built-in formula for finding the vertex. The calculator will then provide the coordinates of the vertex, which can be used to graph the parabola or solve problems involving the vertex.

Steps to Use a Calculator Tool

Here are the steps to use a calculator tool to find the vertex of a parabola:

1. Enter the values of a, b, and c into the calculator.
2. Use the built-in formula for finding the vertex, which is typically given by the equation (h, k) = (-b/2a, f(-b/2a)).
3. Press the "Calculate" button to find the coordinates of the vertex.
4. Use the coordinates of the vertex to graph the parabola or solve problems involving the vertex.

Example Problems

Here are some example problems that demonstrate how to use a calculator tool to find the vertex of a parabola:

• Find the vertex of the parabola y = 2x^2 + 4x + 1.
• Find the vertex of the parabola y = -3x^2 + 2x - 4.
• Find the vertex of the parabola y = x^2 - 2x + 1.

Solutions

Here are the solutions to the example problems:

• The vertex of the parabola y = 2x^2 + 4x + 1 is (-1, -1).
• The vertex of the parabola y = -3x^2 + 2x - 4 is (1/3, -49/12).
• The vertex of the parabola y = x^2 - 2x + 1 is (1, 0).

Conclusion and Final Thoughts

In conclusion, the vertex form of parabolas is a powerful tool for finding the vertex of a parabola. By using a calculator tool, you can easily find the coordinates of the vertex and use them to graph the parabola or solve problems involving the vertex. We hope this article has provided you with a better understanding of the vertex form of parabolas and how to use a calculator tool to find the vertex of a parabola.

Share Your Thoughts

We would love to hear your thoughts on this article. Have you ever used a calculator tool to find the vertex of a parabola? What are some common challenges you face when working with parabolas? Share your thoughts and experiences in the comments below.