Simplify 52 To A Fraction In Simplest Form

Quick Links :

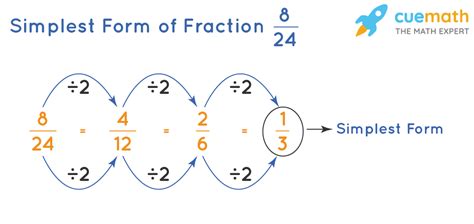
To simplify 52 to a fraction in simplest form, we need to find the greatest common divisor (GCD) of 52 and the denominator, which is 100 in this case, since 52 is a percentage.

First, let's convert 52 to a fraction:

52 = 52/100

Now, let's find the GCD of 52 and 100:

Factors of 52: 1, 2, 4, 13, 26, 52 Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100

The greatest common divisor of 52 and 100 is 4.

Now, let's divide both the numerator and denominator by 4:

52 ÷ 4 = 13 100 ÷ 4 = 25

So, the simplified fraction is:

13/25

Therefore, 52 simplifies to 13/25 in simplest form.

Visual Representation

Benefits of Simplifying Fractions

Simplifying fractions can help in various mathematical operations, such as:

• Easier calculations: Simplified fractions make calculations faster and more accurate.
• Improved understanding: Simplifying fractions helps in understanding the concept of equivalent ratios and proportions.
• Better representation: Simplified fractions provide a clearer representation of the relationship between the numerator and denominator.

Real-World Applications

Simplifying fractions has numerous real-world applications, including:

• Cooking and recipes: Simplified fractions help in measuring ingredients and scaling recipes.
• Finance and budgeting: Simplified fractions are used in calculating interest rates, investments, and expenses.
• Science and engineering: Simplified fractions are essential in calculating proportions, ratios, and scaling factors.

Common Mistakes to Avoid

When simplifying fractions, avoid the following common mistakes:

• Not finding the GCD: Failing to find the greatest common divisor can lead to incorrect simplification.
• Not dividing both numerator and denominator: Dividing only one part of the fraction can result in an incorrect simplification.

By avoiding these common mistakes and following the steps outlined above, you can simplify fractions accurately and confidently.

Practice Problems

Try simplifying the following fractions:

• 48/120
• 75/150
• 24/32

Check your answers and review the steps outlined above to ensure accuracy.

Additional Resources

For more information on simplifying fractions, check out the following resources:

• Khan Academy: Fraction Simplification
• Mathway: Simplifying Fractions
• Purplemath: Simplifying Fractions

These resources provide detailed explanations, examples, and practice problems to help you master the skill of simplifying fractions.

Conclusion

Simplifying fractions is an essential math skill that can help you in various real-world applications. By following the steps outlined above and avoiding common mistakes, you can simplify fractions accurately and confidently. Practice regularly and review the resources provided to become a pro at simplifying fractions!