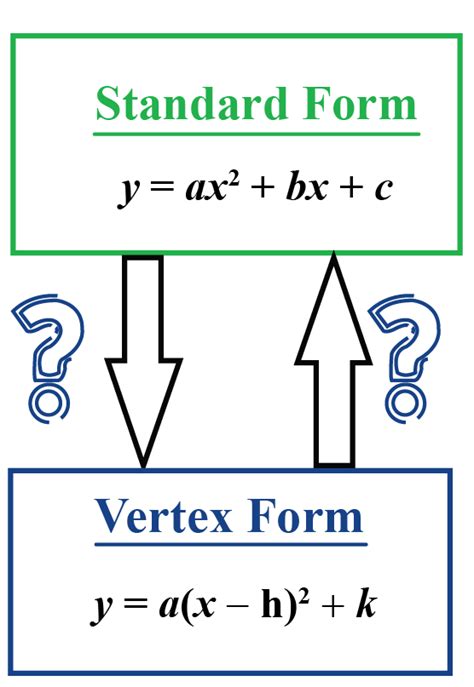
The concept of converting standard form to vertex form is a crucial one in algebra, particularly when dealing with quadratic equations. For those who may be new to this topic, standard form refers to the general equation of a quadratic function, which takes the form ax^2 + bx + c = 0. On the other hand, vertex form, also known as the vertex representation, is a more convenient way of expressing quadratic functions, especially when it comes to graphing and finding key features of the parabola. The vertex form is expressed as a(x - h)^2 + k, where (h, k) represents the coordinates of the vertex of the parabola. In this article, we will delve into the five ways to convert standard form to vertex form.

Understanding the Need for Conversion
Before we dive into the methods of conversion, it's essential to understand why we need to convert standard form to vertex form in the first place. The main advantage of vertex form is that it allows us to easily identify the vertex of the parabola, which is a crucial point in graphing and analyzing quadratic functions. Additionally, vertex form makes it easier to determine the axis of symmetry, the maximum or minimum value of the function, and the direction of opening of the parabola.
Why Vertex Form is Preferred
Vertex form is preferred over standard form for several reasons:
- It provides a clear representation of the vertex of the parabola, making it easier to graph and analyze.
- It allows for easy identification of the axis of symmetry, which is essential for graphing and finding key features of the parabola.
- It makes it easier to determine the maximum or minimum value of the function, which is crucial in optimization problems.
Method 1: Factoring
One of the simplest ways to convert standard form to vertex form is by factoring. This method involves factoring the quadratic expression in standard form and then rewriting it in vertex form.

For example, consider the quadratic function x^2 + 5x + 6 = 0. We can factor this expression as (x + 3)(x + 2) = 0. To rewrite this in vertex form, we need to complete the square. We can do this by adding and subtracting the square of half the coefficient of x to the expression.
x^2 + 5x + 6 = (x + 3)(x + 2) = x^2 + 5x + 25/4 - 25/4 + 6 = (x + 5/2)^2 - 25/4 + 6
Simplifying, we get (x + 5/2)^2 - 1/4, which is in vertex form.
Method 1: Factoring Example
Let's consider another example. Suppose we have the quadratic function x^2 + 3x - 4 = 0. We can factor this expression as (x + 4)(x - 1) = 0. To rewrite this in vertex form, we need to complete the square.
x^2 + 3x - 4 = (x + 4)(x - 1) = x^2 + 3x + 9/4 - 9/4 - 4 = (x + 3/2)^2 - 9/4 - 4
Simplifying, we get (x + 3/2)^2 - 25/4, which is in vertex form.
Method 2: Completing the Square
Another method of converting standard form to vertex form is by completing the square. This method involves adding and subtracting the square of half the coefficient of x to the expression.

For example, consider the quadratic function x^2 + 6x + 8 = 0. To rewrite this in vertex form, we need to complete the square.
x^2 + 6x + 8 = x^2 + 6x + 9 - 9 + 8 = (x + 3)^2 - 1
Simplifying, we get (x + 3)^2 - 1, which is in vertex form.
Method 2: Completing the Square Example
Let's consider another example. Suppose we have the quadratic function x^2 - 4x - 3 = 0. To rewrite this in vertex form, we need to complete the square.
x^2 - 4x - 3 = x^2 - 4x + 4 - 4 - 3 = (x - 2)^2 - 7
Simplifying, we get (x - 2)^2 - 7, which is in vertex form.
Method 3: Using the Formula
A third method of converting standard form to vertex form is by using the formula. The formula for converting standard form to vertex form is a(x - h)^2 + k, where h = -b/2a and k = c - b^2/4a.

For example, consider the quadratic function x^2 + 2x + 1 = 0. To rewrite this in vertex form using the formula, we need to calculate the values of h and k.
h = -b/2a = -2/2 = -1 k = c - b^2/4a = 1 - 2^2/4 = 0
Simplifying, we get (x + 1)^2, which is in vertex form.
Method 3: Using the Formula Example
Let's consider another example. Suppose we have the quadratic function x^2 - 3x - 2 = 0. To rewrite this in vertex form using the formula, we need to calculate the values of h and k.
h = -b/2a = -(-3)/2 = 3/2 k = c - b^2/4a = -2 - (-3)^2/4 = -11/4
Simplifying, we get (x - 3/2)^2 - 11/4, which is in vertex form.
Method 4: Graphing
A fourth method of converting standard form to vertex form is by graphing. This method involves graphing the quadratic function and identifying the vertex of the parabola.

For example, consider the quadratic function x^2 + 4x + 4 = 0. To rewrite this in vertex form by graphing, we need to graph the quadratic function and identify the vertex of the parabola.
The graph of the quadratic function is a parabola that opens upward, and the vertex is at (-2, -4). Therefore, the vertex form of the quadratic function is (x + 2)^2 - 4.
Method 4: Graphing Example
Let's consider another example. Suppose we have the quadratic function x^2 - 2x - 3 = 0. To rewrite this in vertex form by graphing, we need to graph the quadratic function and identify the vertex of the parabola.
The graph of the quadratic function is a parabola that opens downward, and the vertex is at (1, 4). Therefore, the vertex form of the quadratic function is (x - 1)^2 + 4.
Method 5: Using a Calculator
A fifth method of converting standard form to vertex form is by using a calculator. This method involves using a graphing calculator to graph the quadratic function and identify the vertex of the parabola.

For example, consider the quadratic function x^2 + 5x + 6 = 0. To rewrite this in vertex form using a calculator, we need to graph the quadratic function and identify the vertex of the parabola.
Using a graphing calculator, we can graph the quadratic function and identify the vertex as (-5/2, -25/4). Therefore, the vertex form of the quadratic function is (x + 5/2)^2 - 25/4.
Method 5: Using a Calculator Example
Let's consider another example. Suppose we have the quadratic function x^2 - 3x - 2 = 0. To rewrite this in vertex form using a calculator, we need to graph the quadratic function and identify the vertex of the parabola.
Using a graphing calculator, we can graph the quadratic function and identify the vertex as (3/2, -11/4). Therefore, the vertex form of the quadratic function is (x - 3/2)^2 - 11/4.
What is the difference between standard form and vertex form?
+Standard form is the general equation of a quadratic function, while vertex form is a more convenient way of expressing quadratic functions, especially when it comes to graphing and finding key features of the parabola.
Why is vertex form preferred over standard form?
+Vertex form is preferred because it provides a clear representation of the vertex of the parabola, making it easier to graph and analyze.
What are the five methods of converting standard form to vertex form?
+The five methods are factoring, completing the square, using the formula, graphing, and using a calculator.
We hope this article has been helpful in explaining the five ways to convert standard form to vertex form. Whether you're a student or a teacher, understanding these methods is crucial for success in algebra. Remember to practice each method to become proficient in converting standard form to vertex form. If you have any questions or need further clarification, feel free to ask in the comments section below.