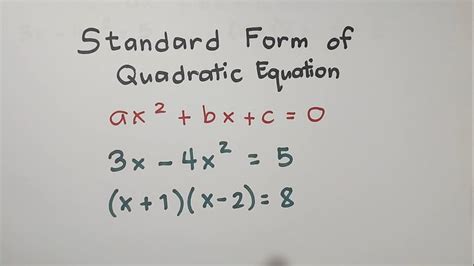Quadratic equations are a fundamental concept in algebra and are used to describe a wide range of phenomena in mathematics, physics, engineering, and other fields. The standard form of a quadratic equation is a crucial concept that provides a powerful tool for solving quadratic equations and graphing parabolas. In this article, we will delve into the world of quadratic equations and explore the standard form, its importance, and its applications.
What is a Quadratic Equation?

A quadratic equation is a polynomial equation of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic equation is:
ax^2 + bx + c = 0
where a, b, and c are constants, and x is the variable. The coefficient "a" cannot be zero, as this would result in a linear equation.
The Standard Form of a Quadratic Equation

The standard form of a quadratic equation is:
ax^2 + bx + c = 0
where a, b, and c are real numbers, and a ≠ 0. This form is also known as the general form of a quadratic equation. The standard form provides a concise way of expressing a quadratic equation and is used as a foundation for solving quadratic equations and graphing parabolas.
Why is the Standard Form Important?
The standard form of a quadratic equation is important because it:
- Provides a consistent way of expressing quadratic equations
- Allows for easy identification of the coefficients a, b, and c
- Enables the use of standard methods for solving quadratic equations, such as factoring, quadratic formula, and graphing
- Facilitates the analysis of the properties of the quadratic equation, such as the vertex, axis of symmetry, and x-intercepts
Components of the Standard Form

The standard form of a quadratic equation consists of three components:
- a: the coefficient of the x^2 term, which cannot be zero
- b: the coefficient of the x term
- c: the constant term
These components provide valuable information about the quadratic equation, such as its vertex, axis of symmetry, and x-intercepts.
How to Write a Quadratic Equation in Standard Form
To write a quadratic equation in standard form, follow these steps:
- Identify the coefficients a, b, and c
- Write the equation in the form ax^2 + bx + c = 0
- Ensure that a ≠ 0
For example, the quadratic equation x^2 + 5x + 6 can be written in standard form as:
x^2 + 5x + 6 = 0
Applications of the Standard Form

The standard form of a quadratic equation has numerous applications in mathematics, physics, engineering, and other fields. Some examples include:
- Solving quadratic equations: the standard form provides a foundation for solving quadratic equations using methods such as factoring, quadratic formula, and graphing
- Graphing parabolas: the standard form enables the graphing of parabolas, which is essential in physics, engineering, and other fields
- Modeling real-world phenomena: quadratic equations are used to model a wide range of real-world phenomena, such as projectile motion, population growth, and electrical circuits
Conclusion
In conclusion, the standard form of a quadratic equation is a fundamental concept in algebra that provides a powerful tool for solving quadratic equations and graphing parabolas. Understanding the standard form is essential for working with quadratic equations and has numerous applications in mathematics, physics, engineering, and other fields.
We hope this article has provided a comprehensive overview of the standard form of a quadratic equation. If you have any questions or comments, please feel free to share them below.
What is the standard form of a quadratic equation?
+The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are real numbers, and a ≠ 0.
Why is the standard form important?
+The standard form provides a consistent way of expressing quadratic equations, enables the use of standard methods for solving quadratic equations, and facilitates the analysis of the properties of the quadratic equation.
What are the components of the standard form?
+The components of the standard form are a, the coefficient of the x^2 term; b, the coefficient of the x term; and c, the constant term.