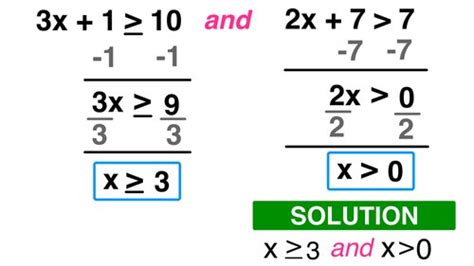
Solving Standard Form Inequality Made Easy

Quick Links :

Solving standard form inequalities is a crucial skill in algebra, and it's essential to master it to tackle more complex math problems. An inequality is a statement that says one expression is greater than, less than, or equal to another expression. Standard form inequalities are written in a specific format, which makes them easier to solve. In this article, we'll break down the steps to solve standard form inequalities and provide examples to help you understand the concept better.

What is a Standard Form Inequality?

A standard form inequality is written in the format:

ax + b > c

or

ax + b < c

or

ax + b ≥ c

or

ax + b ≤ c

where a, b, and c are real numbers, and x is the variable. The goal is to isolate the variable x and find the solution set.

How to Solve Standard Form Inequality?

To solve a standard form inequality, follow these steps:

1. Add or subtract the same value to both sides: If there's a constant term on the same side as the variable, add or subtract it to isolate the variable.
2. Multiply or divide both sides by the same value: If there's a coefficient (a number multiplied by the variable), multiply or divide both sides by the reciprocal of the coefficient to isolate the variable.
3. Flip the inequality sign: If you multiply or divide both sides by a negative number, flip the inequality sign.

Examples of Solving Standard Form Inequalities

Let's solve some examples to illustrate the steps:

Example 1: Solve the inequality 2x + 3 > 5

Solution:

1. Subtract 3 from both sides: 2x > 2
2. Divide both sides by 2: x > 1

Example 2: Solve the inequality x - 2 < 4

Solution:

1. Add 2 to both sides: x < 6

Example 3: Solve the inequality 3x - 2 ≥ 2

Solution:

1. Add 2 to both sides: 3x ≥ 4
2. Divide both sides by 3: x ≥ 4/3

Tips and Tricks

• Always check your solution by plugging it back into the original inequality.
• Be careful when multiplying or dividing both sides by a negative number, as it flips the inequality sign.
• Use a number line to visualize the solution set.

Graphing Standard Form Inequalities

Graphing inequalities on a number line can help you visualize the solution set. To graph an inequality, follow these steps:

1. Plot the boundary point: If the inequality is ≥ or ≤, plot a closed circle on the number line. If the inequality is > or <, plot an open circle.
2. Shade the region: Shade the region above or below the boundary point, depending on the inequality sign.

Real-World Applications

Standard form inequalities are used in various real-world applications, such as:

• Optimization problems: finding the maximum or minimum value of a function.
• Resource allocation: allocating resources, such as money or time, to meet certain constraints.
• Physics and engineering: modeling real-world phenomena, such as the motion of objects.

Conclusion

Solving standard form inequalities is a fundamental skill in algebra. By following the steps outlined in this article, you'll be able to solve standard form inequalities with ease. Remember to always check your solution, use a number line to visualize the solution set, and apply the skills to real-world problems.

FAQ