5 Ways To Master Standard Form Ax+By=C

Quick Links :

Mastering standard form, also known as Ax + By = C, is a crucial skill in mathematics, particularly in algebra and geometry. It's a fundamental concept that helps solve various problems, from simple linear equations to complex systems of equations. In this article, we'll explore five ways to master standard form and become proficient in working with Ax + By = C.

Understanding the Basics of Standard Form

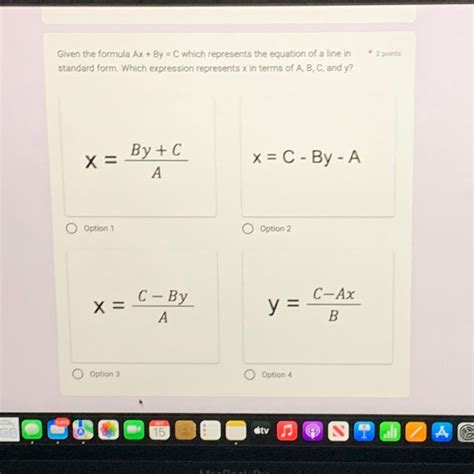
Standard form is a way of representing linear equations in the form Ax + By = C, where A, B, and C are constants, and x and y are variables. The coefficients A and B represent the slope and y-intercept of the line, respectively. To master standard form, it's essential to understand the basic concepts of linear equations, including slope, y-intercept, and graphing lines.

Key Concepts to Remember

• Slope (A): represents the rate of change of the line
• Y-intercept (B): represents the point where the line intersects the y-axis
• Coefficient (C): represents the constant term in the equation

Method 1: Graphing Lines in Standard Form

Graphing lines in standard form is an excellent way to visualize the equation and understand its components. To graph a line in standard form, follow these steps:

1. Plot the y-intercept (B) on the y-axis.
2. Use the slope (A) to find another point on the line.
3. Draw a line through the two points.

By graphing lines in standard form, you can see the relationship between the coefficients and the line's slope and y-intercept.

Method 2: Converting to Slope-Intercept Form

Converting standard form to slope-intercept form (y = mx + b) is a useful technique for solving linear equations. To convert, follow these steps:

1. Divide both sides of the equation by B.
2. Rearrange the equation to isolate y.

Slope-intercept form makes it easy to identify the slope and y-intercept, making it a powerful tool for solving linear equations.

Method 3: Solving Systems of Equations

Solving systems of equations is a crucial application of standard form. To solve a system of linear equations, follow these steps:

1. Write both equations in standard form.
2. Multiply one or both equations by necessary multiples to make the coefficients of x or y the same.
3. Add or subtract the equations to eliminate one variable.
4. Solve for the remaining variable.

Mastering systems of equations requires a deep understanding of standard form and the ability to manipulate equations to solve complex problems.

Method 4: Using Standard Form to Find the Equation of a Line

Given two points on a line, you can use standard form to find the equation of the line. To do this, follow these steps:

1. Use the two points to find the slope (A).
2. Use the slope and one point to find the y-intercept (B).
3. Write the equation in standard form.

This method is essential for finding the equation of a line given two points, a common problem in geometry and trigonometry.

Method 5: Practicing with Real-World Applications

Practicing with real-world applications is an excellent way to master standard form. Try solving problems that involve linear equations, such as:

• Cost calculations: finding the total cost of goods based on the quantity and price per unit
• Distance and rate problems: finding the distance traveled or time taken based on the rate and time
• Physics and engineering: modeling real-world phenomena using linear equations

By practicing with real-world applications, you'll develop a deeper understanding of standard form and its applications in various fields.

By mastering standard form, you'll develop a strong foundation in linear equations and be able to solve a wide range of problems in mathematics and other fields. Practice regularly, and don't hesitate to ask for help when you need it. With persistence and dedication, you'll become proficient in working with Ax + By = C and be able to tackle complex problems with confidence.