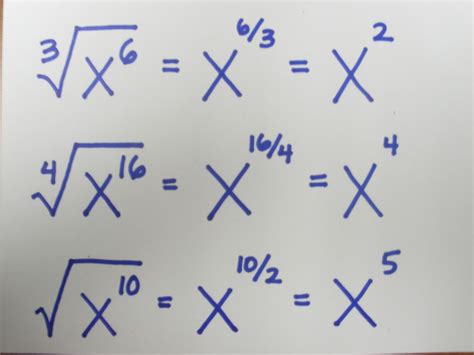5 Ways To Express Square Root Of X Exponentially

Quick Links :

The concept of square roots and exponents is fundamental in mathematics, particularly in algebra and calculus. Understanding how to express square roots of x exponentially is crucial for solving complex equations and manipulating expressions. In this article, we will explore five ways to express the square root of x exponentially.

What is the Square Root of X?

The square root of x, denoted by √x or x^(1/2), is a value that, when multiplied by itself, gives the original value x. In other words, √x is a number that, when squared, equals x. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16.

Method 1: Using Exponentiation

One way to express the square root of x exponentially is to use the exponentiation operator. In this method, we can rewrite the square root of x as x raised to the power of 1/2.

x^(1/2) = √x

This method is straightforward and easy to understand, as it involves simply raising x to the power of 1/2 to obtain its square root.

Method 2: Using Radical Notation

Another way to express the square root of x exponentially is to use radical notation. In this method, we can rewrite the square root of x as x raised to the power of 1/2, but with a radical sign (√) instead of the exponentiation operator.

√x = x^(1/2)

This method is commonly used in mathematical expressions and equations, as it provides a clear and concise way to represent the square root of x.

Method 3: Using Logarithms

A more advanced way to express the square root of x exponentially is to use logarithms. In this method, we can rewrite the square root of x as the logarithm of x to the base of e, where e is the base of the natural logarithm.

√x = e^(ln(x)/2)

This method involves using the natural logarithm (ln) of x and dividing it by 2, then raising e to that power to obtain the square root of x.

Method 4: Using Trigonometry

Another way to express the square root of x exponentially is to use trigonometry. In this method, we can rewrite the square root of x as the cosine of the angle whose sine is x.

√x = cos( arcsin(x) )

This method involves using the inverse sine (arcsin) of x to obtain the angle whose cosine is the square root of x.

Method 5: Using Hyperbolic Functions

A more specialized way to express the square root of x exponentially is to use hyperbolic functions. In this method, we can rewrite the square root of x as the hyperbolic sine (sinh) of the natural logarithm of x.

√x = sinh( ln(x) )

This method involves using the natural logarithm (ln) of x and taking the hyperbolic sine of that value to obtain the square root of x.

Conclusion

Expressing the square root of x exponentially is a fundamental concept in mathematics, with various methods available to suit different needs and applications. The five methods presented in this article provide a range of approaches to rewrite the square root of x exponentially, from simple exponentiation to more advanced logarithmic and trigonometric methods.

We hope this article has provided you with a deeper understanding of how to express the square root of x exponentially. Whether you are a student, teacher, or researcher, we encourage you to share your thoughts and experiences with us in the comments section below.