Simplify Square Roots In 1 Easy Way

Square roots are a fundamental concept in mathematics, and simplifying them is an essential skill for students, teachers, and professionals alike. However, many people struggle with simplifying square roots, especially when it comes to complex expressions. In this article, we will explore a simple and effective method for simplifying square roots, making it easier for you to tackle even the most challenging problems.
Simplifying square roots is a crucial step in various mathematical operations, such as solving equations, finding derivatives, and calculating areas and volumes. Despite its importance, many people find simplifying square roots to be a daunting task. The good news is that there is a straightforward way to simplify square roots, and it's easier than you think.
The key to simplifying square roots lies in understanding the concept of perfect squares. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. For example, 16 is a perfect square because it can be expressed as 4 × 4. Similarly, 25 is a perfect square because it can be expressed as 5 × 5. When simplifying square roots, it's essential to identify perfect squares within the expression.
How to Simplify Square Roots in 1 Easy Way

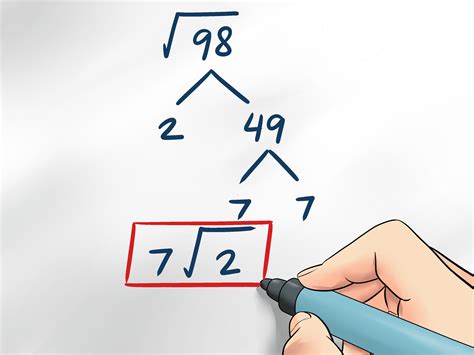
The simple method for simplifying square roots involves factoring the expression inside the square root sign into perfect squares. Here's the step-by-step process:
- Factor the expression inside the square root sign into prime factors.
- Identify perfect squares within the expression.
- Simplify the expression by taking the square root of the perfect squares.
Let's consider an example to illustrate this method. Suppose we want to simplify the expression √(48). To simplify this expression, we follow the steps outlined above:
- Factor the expression inside the square root sign into prime factors: 48 = 2 × 2 × 2 × 2 × 3.
- Identify perfect squares within the expression: We can see that 16 is a perfect square (2 × 2 × 2 × 2).
- Simplify the expression by taking the square root of the perfect squares: √(48) = √(16 × 3) = √16 × √3 = 4√3.
As you can see, simplifying square roots using this method is a breeze. By factoring the expression inside the square root sign into perfect squares, you can simplify even the most complex expressions with ease.
Benefits of Simplifying Square Roots

Simplifying square roots has numerous benefits, especially in mathematical and scientific applications. Here are some of the advantages of simplifying square roots:
- Improved accuracy: Simplifying square roots ensures that you obtain accurate results, which is critical in mathematical and scientific calculations.
- Increased efficiency: By simplifying square roots, you can reduce the complexity of expressions, making it easier to perform calculations and solve problems.
- Better understanding: Simplifying square roots helps you understand the underlying mathematical concepts, making it easier to grasp complex ideas and relationships.
- Enhanced problem-solving skills: By mastering the art of simplifying square roots, you can develop your problem-solving skills, enabling you to tackle more challenging problems with confidence.
Common Mistakes to Avoid When Simplifying Square Roots

When simplifying square roots, it's essential to avoid common mistakes that can lead to incorrect results. Here are some common pitfalls to watch out for:
- Incorrect factoring: Make sure to factor the expression inside the square root sign correctly, as incorrect factoring can lead to incorrect results.
- Missing perfect squares: Be sure to identify all perfect squares within the expression, as missing one can result in an incorrect simplification.
- Incorrect simplification: Double-check your simplification to ensure that you have taken the square root of the perfect squares correctly.
By avoiding these common mistakes, you can ensure that your simplifications are accurate and reliable.
Real-World Applications of Simplifying Square Roots

Simplifying square roots has numerous real-world applications, including:
- Physics and engineering: Simplifying square roots is essential in calculating distances, velocities, and accelerations in physics and engineering.
- Computer science: Simplifying square roots is used in computer graphics, game development, and scientific simulations.
- Finance: Simplifying square roots is used in financial modeling, risk analysis, and option pricing.
- Mathematics: Simplifying square roots is a fundamental skill in mathematics, essential for solving equations, finding derivatives, and calculating areas and volumes.
In conclusion, simplifying square roots is a crucial skill that can make a significant difference in your mathematical and scientific pursuits. By mastering the simple method outlined in this article, you can simplify even the most complex expressions with ease. Remember to avoid common mistakes and apply simplifying square roots to real-world applications to reap the benefits of this essential skill.
Share Your Thoughts!
What are your experiences with simplifying square roots? Do you have any favorite tips or tricks for simplifying complex expressions? Share your thoughts in the comments section below!
What is the purpose of simplifying square roots?
+The purpose of simplifying square roots is to reduce complex expressions into simpler forms, making it easier to perform calculations and solve problems.
How do I simplify a square root expression?
+To simplify a square root expression, factor the expression inside the square root sign into perfect squares, and then take the square root of the perfect squares.
What are some common mistakes to avoid when simplifying square roots?
+