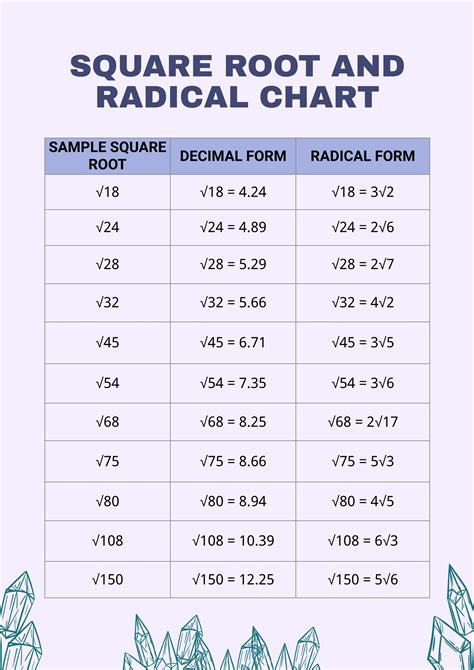
The square root of 65 is a mathematical concept that has fascinated mathematicians and students alike for centuries. In this article, we will delve into the world of radicals and explore the simplest radical form of the square root of 65.
What is the Square Root of 65?

The square root of 65 is a number that, when multiplied by itself, gives the result of 65. In mathematical terms, it can be represented as √65. The square root of 65 is an irrational number, which means it cannot be expressed as a finite decimal or fraction.
Why is the Square Root of 65 Important?
The square root of 65 has numerous applications in mathematics, science, and engineering. It is used to solve equations, calculate distances, and determine the size of shapes. For instance, in geometry, the square root of 65 can be used to find the length of the diagonal of a rectangle with sides of 5 and 13 units.
Simplest Radical Form of the Square Root of 65

To express the square root of 65 in its simplest radical form, we need to find the largest perfect square that divides 65. The prime factorization of 65 is 5 × 13. Since 5 and 13 are not perfect squares, we cannot simplify the square root of 65 further.
However, we can express the square root of 65 as a product of two square roots:
√65 = √(5 × 13) = √5 × √13
This is the simplest radical form of the square root of 65.
Benefits of Simplifying Radicals
Simplifying radicals has several benefits in mathematics. It helps to:
- Reduce the complexity of equations and expressions
- Make calculations easier and faster
- Improve the accuracy of mathematical models
- Enhance the understanding of mathematical concepts
Real-World Applications of the Square Root of 65

The square root of 65 has numerous real-world applications in:
- Architecture: to calculate the height of buildings and the length of shadows
- Engineering: to determine the size of mechanical components and the stress on materials
- Physics: to calculate the distance and velocity of objects in motion
- Computer Science: to optimize algorithms and improve the performance of computer programs
Practical Examples
Here are some practical examples of the square root of 65 in action:
- A carpenter needs to calculate the length of a diagonal beam in a roof. If the beam is 5 feet long and the roof is 13 feet wide, the carpenter can use the square root of 65 to determine the length of the diagonal beam.
- A physicist wants to calculate the distance a car travels in 5 seconds. If the car is traveling at a speed of 13 meters per second, the physicist can use the square root of 65 to determine the distance traveled.
Conclusion and Future Directions

In conclusion, the square root of 65 is an important mathematical concept with numerous applications in science, engineering, and mathematics. By simplifying radicals, we can make calculations easier, improve accuracy, and enhance our understanding of mathematical concepts. As we continue to explore the world of mathematics, we will undoubtedly discover new and exciting applications of the square root of 65.
We invite you to share your thoughts and comments on the square root of 65 and its applications. How do you use the square root of 65 in your daily life or work? What are some other interesting applications of this mathematical concept?
What is the square root of 65?
+The square root of 65 is an irrational number that, when multiplied by itself, gives the result of 65.
Why is the square root of 65 important?
+The square root of 65 has numerous applications in mathematics, science, and engineering, including solving equations, calculating distances, and determining the size of shapes.
How can I simplify the square root of 65?
+To simplify the square root of 65, we need to find the largest perfect square that divides 65. The prime factorization of 65 is 5 × 13. Since 5 and 13 are not perfect squares, we cannot simplify the square root of 65 further.