Simple Fraction Addition Made Easy

Quick Links :

Adding fractions can seem like a daunting task, especially when the denominators are different. However, with a few simple steps and some practice, you can master the art of fraction addition. In this article, we will explore the basics of fraction addition, provide examples, and offer tips to make the process easier.

Fraction addition is an essential math skill that is used in various real-life applications, such as cooking, science, and finance. Being able to add fractions accurately can help you to solve problems and make informed decisions. Moreover, understanding fraction addition can also help you to build a strong foundation in mathematics, which is essential for advanced math concepts.

In this article, we will delve into the world of fraction addition, covering the basics, common mistakes, and practical examples. We will also provide you with tips and tricks to make fraction addition easier and more manageable.

Understanding Fractions

Before we dive into fraction addition, it is essential to understand what fractions are. A fraction is a way of expressing a part of a whole as a ratio of two numbers. The top number, known as the numerator, represents the number of equal parts that you have, while the bottom number, known as the denominator, represents the total number of parts.

For example, the fraction 1/2 represents one equal part out of a total of two parts. You can think of it as having one slice of pizza out of a total of two slices.

Types of Fractions

There are several types of fractions, including:

• Proper fractions: These are fractions where the numerator is less than the denominator. Examples include 1/2, 3/4, and 2/3.
• Improper fractions: These are fractions where the numerator is greater than or equal to the denominator. Examples include 3/2, 5/4, and 7/3.
• Mixed fractions: These are fractions that consist of a whole number and a proper fraction. Examples include 2 1/2, 3 3/4, and 1 2/3.

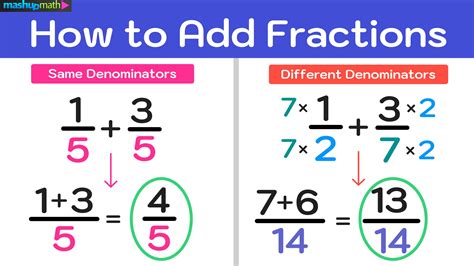
Adding Fractions with the Same Denominator

Adding fractions with the same denominator is a straightforward process. To add two fractions with the same denominator, simply add the numerators and keep the denominator the same.

For example, let's add 1/4 and 3/4:

1/4 + 3/4 = 4/4

Since the denominator is the same, we can simply add the numerators and keep the denominator the same.

Example Problems

• 2/5 + 1/5 =?
• 3/8 + 2/8 =?
• 1/2 + 3/2 =?

Solutions:

• 2/5 + 1/5 = 3/5
• 3/8 + 2/8 = 5/8
• 1/2 + 3/2 = 4/2 = 2

Adding Fractions with Different Denominators

Adding fractions with different denominators requires a few more steps. To add two fractions with different denominators, we need to find the least common multiple (LCM) of the two denominators.

The LCM is the smallest number that both denominators can divide into evenly. Once we have the LCM, we can convert both fractions to have the same denominator, and then add the numerators.

For example, let's add 1/4 and 1/6:

• Find the LCM of 4 and 6, which is 12.
• Convert both fractions to have a denominator of 12: 1/4 = 3/12 and 1/6 = 2/12.
• Add the numerators: 3/12 + 2/12 = 5/12.

Example Problems

• 1/3 + 2/5 =?
• 2/7 + 3/9 =?
• 3/4 + 1/6 =?

Solutions:

• 1/3 + 2/5 = 5/15 + 6/15 = 11/15
• 2/7 + 3/9 = 18/63 + 21/63 = 39/63
• 3/4 + 1/6 = 9/12 + 2/12 = 11/12

Common Mistakes to Avoid

When adding fractions, there are a few common mistakes to avoid:

• Adding the denominators instead of finding the LCM.
• Forgetting to convert both fractions to have the same denominator.
• Adding the numerators instead of the denominators.

To avoid these mistakes, make sure to:

• Always find the LCM of the two denominators.
• Convert both fractions to have the same denominator.
• Add the numerators correctly.

Practical Applications of Fraction Addition

Fraction addition has many practical applications in real-life situations. Here are a few examples:

• Cooking: When following a recipe, you may need to add fractions of ingredients together. For example, if a recipe calls for 1/4 cup of flour and 1/2 cup of sugar, you need to add 1/4 + 1/2 = 3/4 cup.
• Science: In science, fractions are used to express measurements and quantities. For example, if you need to add 1/2 cup of water and 1/4 cup of oil to a mixture, you need to add 1/2 + 1/4 = 3/4 cup.
• Finance: In finance, fractions are used to express interest rates and investment returns. For example, if you have a savings account with an interest rate of 1/4% and a certificate of deposit with an interest rate of 1/2%, you need to add 1/4% + 1/2% = 3/4%.

By mastering fraction addition, you can solve problems and make informed decisions in various real-life situations.

Conclusion

In conclusion, fraction addition is an essential math skill that can seem daunting at first, but with practice and patience, you can master it. By understanding the basics of fractions, finding the LCM, and converting fractions to have the same denominator, you can add fractions with ease.

Remember to avoid common mistakes, such as adding the denominators instead of finding the LCM, and forgetting to convert both fractions to have the same denominator.

Fraction addition has many practical applications in real-life situations, including cooking, science, and finance. By mastering fraction addition, you can solve problems and make informed decisions in various situations.

We hope this article has helped you to understand fraction addition and has provided you with the confidence to tackle fraction problems with ease. If you have any questions or comments, please feel free to share them below.