Square Root Of 40 In Radical Form Simplified

Quick Links :

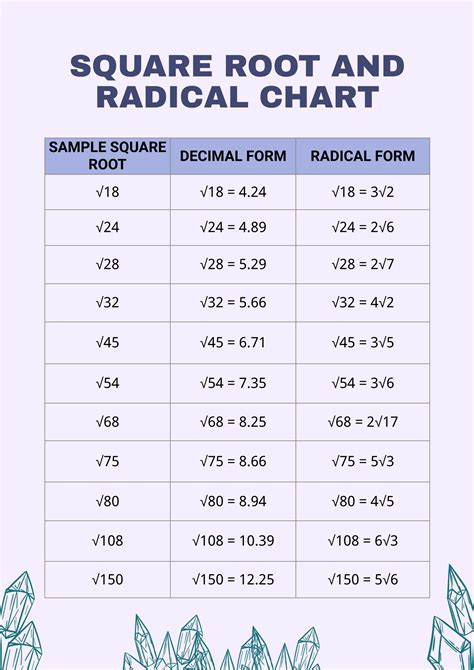
The concept of square roots is a fundamental aspect of mathematics, particularly in algebra and geometry. A square root of a number is a value that, when multiplied by itself, gives the original number. In this article, we will delve into the world of square roots, specifically focusing on the square root of 40 in radical form simplified.

Understanding Square Roots

Before we dive into the specifics of the square root of 40, it's essential to grasp the basics of square roots. A square root of a number x is denoted by the symbol √x. For instance, the square root of 16 is 4, because 4 multiplied by 4 equals 16. Square roots can be classified into two main categories: perfect squares and irrational numbers. Perfect squares have whole number square roots, whereas irrational numbers have decimal or fractional square roots.

Perfect Squares and Irrational Numbers

Perfect squares are numbers that can be expressed as the square of an integer. Examples include 1, 4, 9, and 16. On the other hand, irrational numbers are real numbers that cannot be expressed as a finite decimal or fraction. Pi (π) and the square root of 2 are classic examples of irrational numbers.

The Square Root of 40 in Radical Form

Now that we have a basic understanding of square roots, let's explore the square root of 40 in radical form simplified. The square root of 40 can be expressed as √40. To simplify this, we can break down 40 into its prime factors, which are 2 × 2 × 2 × 5. This can be further simplified to 2^3 × 5.

Simplifying the Square Root of 40

To simplify the square root of 40, we can take the square root of the prime factors. The square root of 2^3 is 2√2, and the square root of 5 is √5. Therefore, the simplified form of the square root of 40 is 2√10.

Working with Radical Forms

Radical forms are an essential aspect of algebra and mathematics. They allow us to express numbers in a simplified and concise manner. When working with radical forms, it's crucial to follow specific rules and guidelines to ensure accuracy.

Multiplying and Dividing Radical Forms

When multiplying or dividing radical forms, we can combine the numbers inside the radical signs. For instance, the product of √2 and √5 is √10. Similarly, the quotient of √10 and √2 is √5.

Real-World Applications of Square Roots

Square roots have numerous real-world applications across various fields, including physics, engineering, architecture, and finance.

Physics and Engineering

In physics and engineering, square roots are used to calculate distances, velocities, and frequencies. For instance, the square root of the sum of the squares of the legs of a right triangle gives the length of the hypotenuse.

Architecture and Construction

In architecture and construction, square roots are used to calculate the diagonal length of a rectangle or the height of a building. This information is crucial for designing and building structures that are safe and aesthetically pleasing.

Conclusion and Final Thoughts

In conclusion, the square root of 40 in radical form simplified is 2√10. This simplified form allows us to express the number in a concise and easy-to-understand manner. Radical forms are an essential aspect of mathematics, and understanding how to work with them is crucial for solving complex problems.

We hope this article has provided you with a deeper understanding of square roots and their applications. If you have any questions or comments, please feel free to share them below.