Square Root Of 14 In Radical Form Explained

Quick Links :

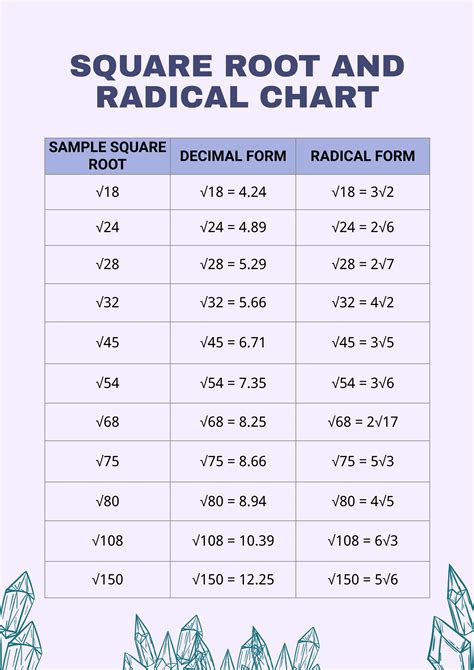
Mathematics has long been a cornerstone of human innovation, and one of the most fundamental concepts in mathematics is the square root. The square root of a number is a value that, when multiplied by itself, gives the original number. One of the most interesting aspects of square roots is when they are expressed in radical form, which can provide a more nuanced understanding of mathematical relationships. In this article, we will delve into the square root of 14 in radical form, exploring its explanation, calculation, and significance.

Understanding Square Roots

Before diving into the specifics of the square root of 14, it's essential to grasp the concept of square roots. A square root of a number is a value that, when multiplied by itself, equals the original number. For instance, the square root of 16 is 4 because 4 multiplied by 4 equals 16. However, not all numbers have a perfect square root, and this is where radical form comes into play.

What is Radical Form?

The radical form of a number represents its square root using a radical symbol (√). This form is particularly useful for expressing square roots of numbers that do not have a perfect square root. For example, the square root of 2 is an irrational number, meaning it cannot be expressed as a simple fraction. Therefore, it is often written in radical form as √2.

Calculating the Square Root of 14

Calculating the square root of 14 is a straightforward process that can be done using a calculator or through estimation. However, to express it in radical form, we need to understand that 14 is not a perfect square. The closest perfect squares are 9 and 16. This means the square root of 14 will fall between the square roots of 9 and 16.

Estimating the Square Root of 14

To estimate the square root of 14, we can consider the square roots of the nearest perfect squares, which are √9 = 3 and √16 = 4. Since 14 falls between 9 and 16, its square root will be between 3 and 4.

Expressing the Square Root of 14 in Radical Form

Given that the square root of 14 is not a perfect square, we express it in radical form as √14. This notation signifies that we are dealing with the square root of an irrational number.

Simplifying Radical Expressions

In some cases, radical expressions can be simplified by factoring out perfect squares. However, the square root of 14 cannot be simplified further because 14 does not contain any perfect square factors other than 1.

Practical Applications of the Square Root of 14

The square root of 14, like other mathematical concepts, has various practical applications in fields such as physics, engineering, and finance. For instance, in physics, square roots are used in equations to describe the motion of objects. In finance, square roots are used in calculations related to volatility and risk.

Real-World Examples

1. Physics: The square root of 14 might be used in equations describing the trajectory of a projectile under certain conditions.
2. Finance: In financial modeling, the square root of time (which could involve numbers like 14 in certain contexts) is crucial for calculating volatility.

Conclusion - The Significance of the Square Root of 14 in Radical Form

In conclusion, the square root of 14, when expressed in radical form as √14, provides a deeper understanding of mathematical concepts that are not always perfectly square. This notation is crucial for expressing relationships in mathematics and has numerous applications across various fields. Understanding the square root of 14 in radical form enhances one's appreciation for the complexity and beauty of mathematics.

We invite you to share your thoughts on the significance of expressing square roots in radical form and how it has helped in your understanding of mathematical concepts. Feel free to comment below and start a discussion.