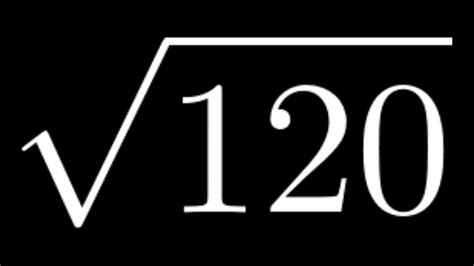Square Root Of 120 In Radical Form Simplified

Quick Links :

The concept of square roots and radical forms is an essential part of mathematics, particularly in algebra and geometry. In this article, we will delve into the world of square roots, exploring what they are, how they are simplified, and specifically, we will simplify the square root of 120 in radical form.

Mathematics is a universal language that helps us describe the world around us, from the simplest shapes to the most complex systems. At the heart of mathematics lies the concept of square roots, which is fundamental in solving equations and understanding geometric shapes. The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 16 is 4 because 4 multiplied by 4 equals 16.

Simplifying square roots, especially those that are not perfect squares, often involves expressing them in radical form. The radical form of a square root is a way of expressing the square root of a number using the radical symbol (√). When simplifying square roots, we aim to find the largest perfect square that divides the number under the radical symbol. This process helps in simplifying complex expressions and solving equations.

Now, let's focus on simplifying the square root of 120 in radical form.

Simplifying Square Roots

To simplify the square root of 120, we look for the largest perfect square that divides 120. Breaking down 120, we can see that it is equal to 2 * 2 * 2 * 3 * 5. Grouping the pairs, we get (2 * 2) * 2 * 3 * 5, which simplifies to 4 * 2 * 3 * 5.

Radical Form Simplification

The square root of 120 can thus be expressed as √(4 * 2 * 3 * 5). Since 4 is a perfect square, we can simplify this further by pulling the 4 out of the radical, resulting in 2√(2 * 3 * 5). Simplifying the product inside the radical, we get 2√30.

The Importance of Radical Form

Expressing square roots in radical form is crucial in mathematics for several reasons. It allows for the simplification of complex expressions, making them easier to work with. Additionally, radical forms provide a standardized way of expressing square roots, which is essential for solving equations and inequalities.

The ability to simplify square roots into radical form also opens up a world of mathematical exploration, enabling students and mathematicians alike to delve deeper into advanced topics such as calculus and algebra. Understanding how to simplify square roots is a foundational skill that builds upon the basic principles of mathematics, serving as a stepping stone for more advanced mathematical concepts.

Practical Applications

Simplifying square roots in radical form has numerous practical applications across various fields. In physics, understanding radical forms is essential for calculating distances, velocities, and accelerations. In engineering, radical forms play a crucial role in the design of buildings, bridges, and electronic circuits. Even in computer science, simplifying square roots is fundamental for algorithms related to geometry and computer graphics.

In conclusion, the square root of 120 in radical form simplified is 2√30. This simplification process not only demonstrates the power of expressing square roots in radical form but also highlights the importance of this concept in mathematics and its real-world applications. Whether in academia or professional fields, understanding how to simplify square roots in radical form is an invaluable skill that opens doors to a deeper appreciation and application of mathematics.

Call to Action

We invite you to share your experiences or questions about simplifying square roots in radical form. How have you applied this concept in your studies or professional life? Share your insights in the comments section below.