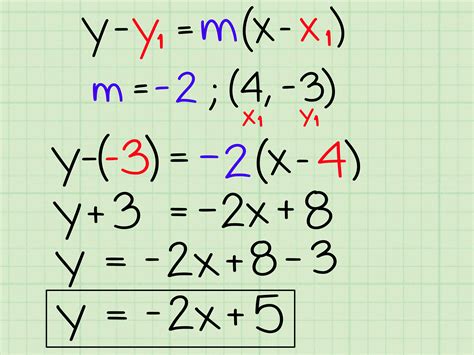5 Easy Steps To Rewrite Equations In Slope Intercept Form

Quick Links :

Rewriting equations in slope-intercept form is a fundamental skill in algebra, and it's essential to understand the process to work with linear equations effectively. The slope-intercept form of a linear equation is y = mx + b, where m is the slope of the line, and b is the y-intercept. In this article, we'll break down the process into 5 easy steps to rewrite equations in slope-intercept form.

Understanding the Importance of Slope-Intercept Form

Slope-intercept form is a popular way to express linear equations because it provides valuable information about the line's slope and y-intercept. The slope (m) represents the rate of change of the line, while the y-intercept (b) indicates the point where the line crosses the y-axis. By rewriting equations in slope-intercept form, you can easily identify these critical components and work with the equation more efficiently.

Step 1: Identify the Given Equation

The first step is to identify the given equation and determine its current form. The equation might be in standard form (ax + by = c), point-slope form (y - y1 = m(x - x1)), or another form. Take note of the variables, coefficients, and constants in the equation.

Example: 2x + 3y = 7

In this example, the equation is in standard form. We have the variables x and y, coefficients 2 and 3, and a constant term 7.

Step 2: Isolate the y-Variable

To rewrite the equation in slope-intercept form, we need to isolate the y-variable. This means getting y by itself on one side of the equation. We can do this by adding or subtracting the same value to both sides of the equation, or by multiplying or dividing both sides by a coefficient.

Example: 2x + 3y = 7

To isolate y, we'll subtract 2x from both sides of the equation:

3y = -2x + 7

Next, we'll divide both sides by 3 to solve for y:

y = (-2/3)x + 7/3

Step 3: Identify the Slope (m)

Now that we have the equation in a form that's close to slope-intercept form, we can identify the slope (m). The slope is the coefficient of the x-variable. In our example, the slope is -2/3.

Step 4: Identify the y-Intercept (b)

The y-intercept (b) is the constant term in the equation. In our example, the y-intercept is 7/3.

Step 5: Write the Equation in Slope-Intercept Form

Now that we have identified the slope (m) and y-intercept (b), we can write the equation in slope-intercept form:

y = (-2/3)x + 7/3

This is the final form of the equation in slope-intercept form.

By following these 5 easy steps, you can rewrite equations in slope-intercept form and gain a deeper understanding of linear equations. Remember to practice, practice, practice to become proficient in rewriting equations in slope-intercept form.

We hope this article has helped you understand the process of rewriting equations in slope-intercept form. If you have any questions or need further clarification, please don't hesitate to ask. Share this article with your friends and classmates who may find it helpful.