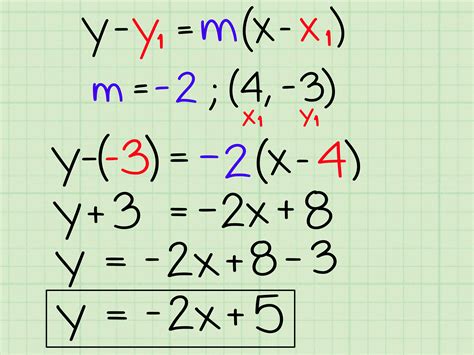Graphing and analyzing linear equations are fundamental skills in mathematics, and one of the most efficient ways to represent these equations is through the slope-intercept form. The slope-intercept form, which is expressed as y = mx + b, where m is the slope and b is the y-intercept, offers a straightforward method for identifying key points on the line, including the x-intercept.
Understanding Slope-Intercept Form

The slope-intercept form, y = mx + b, provides immediate insight into the line's slope (m) and its y-intercept (b). The slope (m) indicates the steepness of the line and whether it slopes upward or downward, while the y-intercept (b) is the point at which the line crosses the y-axis. However, when it comes to finding the x-intercept, the slope-intercept form alone does not provide a direct answer, but it sets the stage for an easy calculation.
What is the X-Intercept?
The x-intercept is the point at which the line crosses the x-axis. By definition, at any point on the x-axis, y = 0. Therefore, to find the x-intercept of a line given in slope-intercept form, one needs to set y to 0 and solve for x.
Calculating the X-Intercept from Slope-Intercept Form

Given the equation y = mx + b, to find the x-intercept, follow these steps:
- Set y to 0: Replace y with 0 in the equation to represent the point on the x-axis.
- Solve for x: The equation now looks like 0 = mx + b. To solve for x, subtract b from both sides of the equation and then divide by m.
Mathematically, this translates to:
0 = mx + b
- b = mx x = -b / m
This formula provides the x-intercept of the line.
Example
Consider the equation y = 2x - 3. To find its x-intercept:
- Set y to 0: 0 = 2x - 3
- Solve for x: Add 3 to both sides and then divide by 2 3 = 2x x = 3 / 2 x = 1.5
Therefore, the x-intercept of the line y = 2x - 3 is (1.5, 0).
Practical Applications of Finding X-Intercept

Finding the x-intercept has numerous practical applications across various fields, including physics, economics, and engineering. For instance, in physics, the x-intercept can represent the time it takes for an object to reach a certain position or the distance traveled under the influence of a constant force. In economics, x-intercepts can help determine the point at which the supply and demand curves intersect, indicating the market equilibrium.
FAQs
- What does the x-intercept represent? The x-intercept is the point at which a line crosses the x-axis, indicating the value of x when y = 0.
- How do you find the x-intercept from the slope-intercept form? To find the x-intercept, set y to 0 in the equation y = mx + b and solve for x.
- What is the significance of the x-intercept in real-world applications? The x-intercept can represent critical values or points of interest in various fields such as physics, economics, and engineering, providing insights into phenomena or trends.
What is the slope-intercept form of a linear equation?
+The slope-intercept form is expressed as y = mx + b, where m is the slope and b is the y-intercept.
Why is finding the x-intercept important?
+Finding the x-intercept can provide valuable insights into real-world phenomena and trends, and is crucial for graphing and analyzing linear equations.
Can the x-intercept be found for any linear equation?
+Yes, the x-intercept can be found for any linear equation by setting y to 0 and solving for x, regardless of the form of the equation.
In conclusion, finding the x-intercept from the slope-intercept form is a straightforward yet powerful tool for analyzing linear equations. By understanding and applying this method, one can unlock a deeper understanding of linear relationships and their real-world applications.
We hope this article has provided you with a comprehensive understanding of finding the x-intercept with the slope-intercept form. If you have any further questions or would like to discuss more on this topic, please feel free to comment below or share this article with your peers.