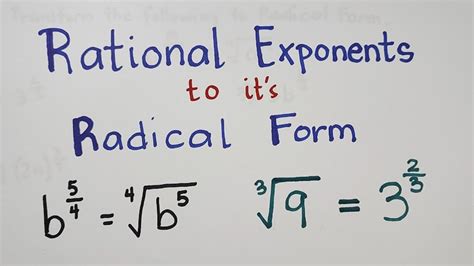Converting Radical Form To Rational Exponent Form Made Easy

Quick Links :

Expressing numbers in different forms can be incredibly useful in mathematics, especially when it comes to calculations and solving equations. One such conversion that is commonly used is converting numbers from radical form to rational exponent form. In this article, we will explore the process of converting radical form to rational exponent form, making it easy for you to grasp and apply this concept.

Radical form is a way of expressing numbers that involves square roots, cube roots, and other higher-order roots. Rational exponent form, on the other hand, is a way of expressing numbers using exponents, where the exponent is a fraction. Both forms are useful in different mathematical contexts, and being able to convert between them can be very helpful.

Understanding Radical Form

Before we dive into the conversion process, let's take a moment to understand radical form. Radical form involves expressing numbers as roots, where the root can be square, cube, or any other higher-order root. For example, √4 is the square root of 4, and ³√27 is the cube root of 27. Radical form can be written in different ways, such as:

• √x (square root of x)
• ³√x (cube root of x)
• ⁴√x (fourth root of x)

Radical form is useful when working with numbers that have a clear root, such as perfect squares or perfect cubes.

Understanding Rational Exponent Form

Rational exponent form, on the other hand, involves expressing numbers using exponents, where the exponent is a fraction. Rational exponent form can be written as:

• x^(m/n) (x raised to the power of m/n)

Rational exponent form is useful when working with numbers that have a fractional exponent, such as √x or x^(1/2).

Converting Radical Form to Rational Exponent Form

Now that we have a basic understanding of radical form and rational exponent form, let's explore the process of converting radical form to rational exponent form.

The conversion process involves two main steps:

1. Identify the root and express it as a fractional exponent.
2. Simplify the expression to its simplest form.

Let's consider an example to illustrate this process. Suppose we want to convert √4 to rational exponent form.

Step 1: Identify the root and express it as a fractional exponent.

√4 can be expressed as 4^(1/2), since the square root of 4 is equivalent to 4 raised to the power of 1/2.

Step 2: Simplify the expression to its simplest form.

4^(1/2) is already in its simplest form, so we can write the final answer as 4^(1/2).

Examples and Practice

Let's consider a few more examples to practice converting radical form to rational exponent form:

• √9 = 9^(1/2)
• ³√27 = 27^(1/3)
• ⁴√256 = 256^(1/4)

Notice that the denominator of the fractional exponent is equal to the index of the root. For example, the square root has an index of 2, so the denominator of the fractional exponent is 2.

Tips and Tricks

Here are a few tips and tricks to keep in mind when converting radical form to rational exponent form:

• Make sure to identify the root and express it as a fractional exponent.
• Simplify the expression to its simplest form.
• Use the property of exponents that states x^(m/n) = (x^(1/n))^m.
• Use the property of exponents that states x^(m/n) = x^m / x^n.

Common Mistakes to Avoid

When converting radical form to rational exponent form, there are a few common mistakes to avoid:

• Forgetting to simplify the expression to its simplest form.
• Writing the fractional exponent incorrectly.
• Forgetting to use the properties of exponents.

By following these tips and avoiding common mistakes, you can master the process of converting radical form to rational exponent form.

Real-World Applications

Converting radical form to rational exponent form has many real-world applications, including:

• Calculus and advanced mathematics
• Physics and engineering
• Computer science and programming
• Data analysis and statistics

By mastering this conversion process, you can solve problems more efficiently and accurately in a wide range of fields.

Conclusion

In conclusion, converting radical form to rational exponent form is a valuable skill that can be used in a wide range of mathematical contexts. By following the steps outlined in this article, you can master this conversion process and apply it to solve problems more efficiently and accurately.

We hope this article has been helpful in explaining the process of converting radical form to rational exponent form. If you have any questions or need further clarification, please don't hesitate to ask.