Mastering Parallel Point Slope Form In Algebra

Quick Links :

Hide

Mastering parallel point slope form in algebra is a crucial concept for students to grasp, as it enables them to understand and work with linear equations in a more comprehensive manner. In this article, we will delve into the world of parallel point slope form, exploring its definition, significance, and practical applications.

Algebra is a branch of mathematics that deals with the study of mathematical symbols, equations, and functions. It involves the use of variables, constants, and mathematical operations to solve equations and manipulate expressions. One of the fundamental concepts in algebra is the point slope form, which is used to represent linear equations.

Understanding Point Slope Form

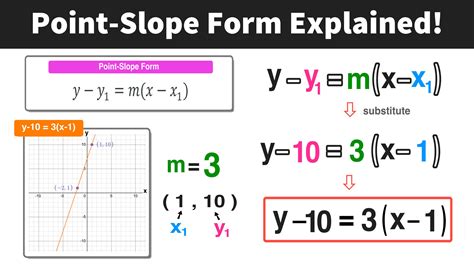
The point slope form is a way of expressing a linear equation in the form y - y1 = m(x - x1), where m is the slope of the line, and (x1, y1) is a point on the line. This form is particularly useful when working with linear equations, as it allows students to easily identify the slope and a point on the line.

Benefits of Using Point Slope Form

There are several benefits to using point slope form when working with linear equations. Some of the advantages include:

• Easy identification of slope and point on the line
• Simplifies the process of graphing linear equations
• Enables students to write linear equations in a more compact form
• Facilitates the process of solving systems of linear equations

What is Parallel Point Slope Form?

Parallel point slope form is a variation of the point slope form that is used to represent two or more linear equations that have the same slope but different y-intercepts. In this form, the equations are written in the form y - y1 = m(x - x1) and y - y2 = m(x - x2), where m is the common slope, and (x1, y1) and (x2, y2) are points on the respective lines.

Significance of Parallel Point Slope Form

Parallel point slope form is a crucial concept in algebra, as it enables students to understand and work with multiple linear equations that have the same slope but different y-intercepts. Some of the significance of parallel point slope form include:

• Enables students to identify and work with multiple linear equations that have the same slope
• Facilitates the process of solving systems of linear equations
• Helps students to understand the concept of parallel lines and their relationship to each other

How to Work with Parallel Point Slope Form

Working with parallel point slope form involves several steps, including:

1. Identify the slope and a point on each line
2. Write the equations in point slope form
3. Identify the common slope and the points on each line
4. Use the common slope and points to write the equations in parallel point slope form
5. Use the equations to solve systems of linear equations

Examples of Working with Parallel Point Slope Form

Here are a few examples of working with parallel point slope form:

Example 1:

Find the equation of the line that passes through the point (2, 3) and has a slope of 2. Write the equation in point slope form.

Solution:

y - 3 = 2(x - 2)

Example 2:

Find the equation of the line that passes through the point (4, 5) and has a slope of 2. Write the equation in point slope form.

Solution:

y - 5 = 2(x - 4)

Example 3:

Find the equation of the line that passes through the point (6, 7) and has a slope of 2. Write the equation in point slope form.

Solution:

y - 7 = 2(x - 6)

Practical Applications of Parallel Point Slope Form

Parallel point slope form has several practical applications in real-life situations, including:

• Physics and engineering: used to model the motion of objects and the forces that act upon them
• Computer science: used to create algorithms and models for solving complex problems
• Economics: used to model the behavior of markets and the impact of economic policies

Common Mistakes to Avoid When Working with Parallel Point Slope Form

When working with parallel point slope form, there are several common mistakes to avoid, including:

• Failing to identify the common slope
• Failing to write the equations in point slope form
• Failing to identify the points on each line
• Failing to use the common slope and points to write the equations in parallel point slope form

Conclusion

Mastering parallel point slope form is a crucial concept in algebra that enables students to understand and work with multiple linear equations that have the same slope but different y-intercepts. By understanding the definition, significance, and practical applications of parallel point slope form, students can improve their algebra skills and solve complex problems with ease.

We hope this article has provided you with a comprehensive understanding of parallel point slope form. If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and experiences with parallel point slope form in the comments section below.