Unlocking the Secrets of Parabolas with a Calculator

Parabolas are one of the most fascinating topics in mathematics, and with the help of a calculator, you can unlock their secrets in just 5 simple steps. Whether you're a student struggling to understand the concept of parabolas or a math enthusiast looking to brush up on your skills, this article will guide you through the process of mastering parabolas using a calculator.
In the world of mathematics, parabolas are a type of quadratic function that has a wide range of applications in fields such as physics, engineering, and economics. However, working with parabolas can be intimidating, especially when it comes to finding the vertex, axis of symmetry, and roots of the parabola. But don't worry, with the help of a calculator, you can simplify the process and become a master of parabolas in no time.
Step 1: Understand the Basics of Parabolas

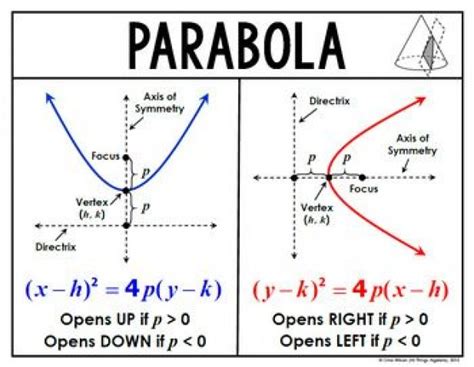
Before we dive into the calculator steps, it's essential to understand the basics of parabolas. A parabola is a quadratic function that can be represented by the equation y = ax^2 + bx + c, where a, b, and c are constants. The parabola opens upwards or downwards depending on the value of 'a'. If 'a' is positive, the parabola opens upwards, and if 'a' is negative, it opens downwards.
The vertex of the parabola is the lowest or highest point, depending on the direction it opens. The axis of symmetry is the vertical line that passes through the vertex and divides the parabola into two equal parts. The roots of the parabola are the points where it intersects the x-axis.
Key Terms to Remember
- Vertex: The lowest or highest point of the parabola
- Axis of symmetry: The vertical line that passes through the vertex
- Roots: The points where the parabola intersects the x-axis
- Quadratic function: A polynomial function of degree two
Step 2: Identify the Quadratic Function

The first step in mastering parabolas with a calculator is to identify the quadratic function. This involves recognizing the equation of the parabola and determining the values of 'a', 'b', and 'c'. For example, let's consider the quadratic function y = 2x^2 + 3x - 4.
Using a calculator, you can enter the values of 'a', 'b', and 'c' and plot the parabola. Most calculators have a built-in quadratic function solver that can help you find the vertex, axis of symmetry, and roots of the parabola.
Tips for Identifying Quadratic Functions
- Look for the coefficient of x^2, which represents the value of 'a'
- Identify the coefficient of x, which represents the value of 'b'
- Determine the constant term, which represents the value of 'c'
Step 3: Find the Vertex and Axis of Symmetry

Once you have identified the quadratic function, the next step is to find the vertex and axis of symmetry. The vertex form of a parabola is y = a(x-h)^2 + k, where (h,k) represents the vertex.
Using a calculator, you can enter the values of 'a', 'b', and 'c' and solve for 'h' and 'k'. The axis of symmetry is the vertical line that passes through the vertex, and its equation is x = h.
Formulas to Remember
- Vertex form: y = a(x-h)^2 + k
- Axis of symmetry: x = h
Step 4: Find the Roots of the Parabola

The final step in mastering parabolas with a calculator is to find the roots of the parabola. The roots of a parabola are the points where it intersects the x-axis.
Using a calculator, you can enter the values of 'a', 'b', and 'c' and solve for the roots. The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a.
Quadratic Formula
- x = (-b ± √(b^2 - 4ac)) / 2a
Step 5: Practice, Practice, Practice

The final step in mastering parabolas with a calculator is to practice, practice, practice. The more you practice, the more comfortable you will become with using a calculator to solve parabolas.
Try solving different types of parabolas, including those that open upwards and downwards. Experiment with different values of 'a', 'b', and 'c' to see how the parabola changes.
Tips for Practicing Parabolas
- Start with simple parabolas and gradually move on to more complex ones
- Experiment with different values of 'a', 'b', and 'c'
- Use online resources or math apps to practice solving parabolas
What is the difference between a parabola and a quadratic function?
+A parabola is a type of quadratic function that has a wide range of applications in fields such as physics, engineering, and economics. A quadratic function is a polynomial function of degree two, and it can be represented by the equation y = ax^2 + bx + c.
How do I find the vertex and axis of symmetry of a parabola using a calculator?
+Using a calculator, you can enter the values of 'a', 'b', and 'c' and solve for 'h' and 'k'. The vertex form of a parabola is y = a(x-h)^2 + k, where (h,k) represents the vertex. The axis of symmetry is the vertical line that passes through the vertex, and its equation is x = h.
What is the quadratic formula, and how do I use it to find the roots of a parabola?
+The quadratic formula is x = (-b ± √(b^2 - 4ac)) / 2a. Using a calculator, you can enter the values of 'a', 'b', and 'c' and solve for the roots. The quadratic formula is used to find the roots of a parabola, which are the points where it intersects the x-axis.
Now that you have mastered the 5 simple steps to unlock the secrets of parabolas with a calculator, it's time to take the next step. Share this article with your friends and classmates, and start practicing solving parabolas using a calculator. With practice and patience, you will become a master of parabolas in no time!