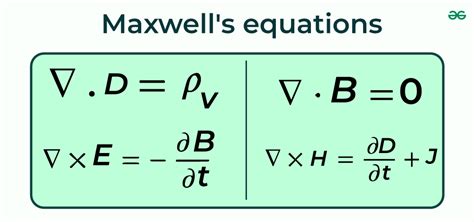Understanding Maxwell's Equations is crucial for anyone interested in the fields of physics, engineering, and mathematics. These four fundamental equations, formulated by James Clerk Maxwell in the 19th century, unify the previously separate theories of electricity and magnetism into a single, coherent theory of electromagnetism. They have far-reaching implications for our understanding of the natural world and have led to countless technological innovations. Here, we will delve into six ways to understand Maxwell's Equations, making them more accessible and providing a comprehensive overview of their significance.
1. Historical Context and Development

To fully appreciate Maxwell's Equations, it's essential to understand the historical context in which they were developed. Before Maxwell, scientists like Michael Faraday and André-Marie Ampère had made significant contributions to the understanding of electricity and magnetism. However, their theories were fragmented and did not provide a unified explanation for the phenomena observed.
Maxwell's breakthrough came when he formulated a set of equations that not only unified the existing theories but also predicted the existence of electromagnetic waves. This was a revolutionary idea, as it posited that light itself was an electromagnetic wave. Experimental verification of this prediction by Heinrich Hertz in the late 19th century confirmed the validity of Maxwell's Equations and cemented their place in the foundation of modern physics.
Key Players and Their Contributions
- Michael Faraday: Contributed significantly to the understanding of electromagnetic induction and introduced the concept of the electromagnetic field.
- André-Marie Ampère: Formulated Ampère's law, which relates the magnetic field around a closed loop to the electric current passing through the loop.
- James Clerk Maxwell: Unified the theories of electricity and magnetism and predicted the existence of electromagnetic waves.
2. Mathematical Formulation

Maxwell's Equations are formulated in terms of vector calculus, specifically using differential equations. There are four equations in total, each addressing a different aspect of electromagnetism:
- Gauss's Law for Electricity: Describes how electric charges produce electric fields.
- Gauss's Law for Magnetism: States that magnetic charges do not exist and magnetic fields are generated by moving charges or changing electric fields.
- Faraday's Law of Induction: Explains how a changing magnetic field induces an electric field.
- Ampère's Law with Maxwell's Addition: Relates the magnetic field to the electric current and the rate of change of the electric field.
These equations can be represented in differential form, which is more useful for solving problems in specific situations, or in integral form, which provides a broader view of the fields and their interactions.
Differential Form of Maxwell's Equations
- ∇⋅E = ρ/ε₀ (Gauss's Law for Electricity)
- ∇⋅B = 0 (Gauss's Law for Magnetism)
- ∇×E = -∂B/∂t (Faraday's Law of Induction)
- ∇×B = μ₀J + μ₀ε₀∂E/∂t (Ampère's Law with Maxwell's Addition)
3. Physical Interpretation

Understanding the physical interpretation of Maxwell's Equations is crucial for applying them in real-world scenarios. Each equation has a direct physical meaning:
- Gauss's Laws: Describe how charges and magnetic fields generate electric and magnetic fields, respectively.
- Faraday's Law: Explains the process of electromagnetic induction, crucial in generators, motors, and transformers.
- Ampère's Law: Shows how electric currents generate magnetic fields.
These interpretations allow us to understand and predict various phenomena, from the operation of electrical devices to the behavior of light and other electromagnetic waves.
4. Applications and Implications

The implications of Maxwell's Equations are vast and profound. They have led to significant technological advancements:
- Electromagnetic Waves: The prediction of electromagnetic waves led to the development of radio communication, radar, and eventually, the internet.
- Electric Power Distribution: Understanding how electric currents generate magnetic fields is crucial for designing electrical generators, motors, and transformers.
- Optics and Photonics: Maxwell's Equations provide the foundation for understanding light and its interactions with matter, which is essential for optics, photonics, and laser technology.
Technological Innovations
- Wireless Communication: Enabled by the understanding of electromagnetic waves.
- Electric Power Systems: Depend on the principles described by Maxwell's Equations.
- Lasers and Photonics: Rely on the understanding of light as an electromagnetic wave.
5. Experimental Verification

The verification of Maxwell's Equations through experiments has been a crucial step in establishing their validity. Key experiments include:
- Heinrich Hertz's Experiments: Demonstrated the existence of electromagnetic waves, confirming Maxwell's prediction.
- Experiments on Electromagnetic Induction: Have consistently supported Faraday's Law of Induction.
- Measurements of the Speed of Light: Have shown that light behaves as an electromagnetic wave, as predicted by Maxwell's Equations.
These experimental verifications have solidified Maxwell's Equations as a cornerstone of physics, with applications that span a wide range of scientific and technological fields.
6. Impact on Modern Physics

Maxwell's Equations have had a profound impact on the development of modern physics. They:
- Unify Electricity and Magnetism: Providing a single framework for understanding electromagnetism.
- Predict Electromagnetic Waves: Leading to a deep understanding of light and other forms of electromagnetic radiation.
- Form the Basis for Quantum Mechanics and Relativity: Maxwell's Equations are a precursor to the development of quantum mechanics and special relativity.
Understanding Maxwell's Equations is not only essential for understanding many phenomena in physics but also for appreciating the beauty of a unified theory that underlies so much of our technological and scientific advancements.
What are Maxwell's Equations?
+Maxwell's Equations are a set of four fundamental equations in classical electromagnetism that describe how electric and magnetic fields interact and how they are generated by charges, currents, and changes in each other.
Why are Maxwell's Equations important?
+Maxwell's Equations are crucial for understanding many phenomena in physics and engineering, including electromagnetic waves, light, and electrical devices. They have led to significant technological advancements and are a foundation for many areas of modern physics.
How were Maxwell's Equations verified experimentally?
+Experiments, notably those by Heinrich Hertz demonstrating the existence of electromagnetic waves, have consistently supported Maxwell's Equations. Measurements and experiments related to electromagnetic induction and the speed of light have also verified the equations.
We hope this comprehensive guide to Maxwell's Equations has not only deepened your understanding of these fundamental laws of physics but also inspired you to explore the vast and fascinating world of electromagnetism. Whether you're a student, a researcher, or simply someone curious about the natural world, Maxwell's Equations offer a doorway to a deeper appreciation of the intricate beauty of the universe.