5 Ways To Multiply Using Expanded Form Easily

Quick Links :

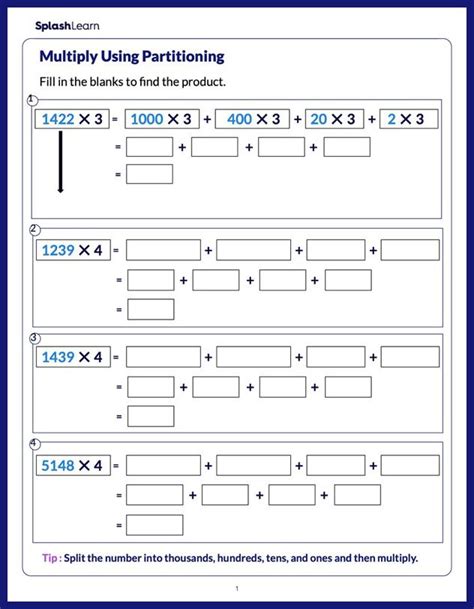
Learning to multiply numbers using expanded form is an essential skill in mathematics, especially when dealing with multi-digit numbers. Expanded form multiplication helps break down the multiplication process into smaller, more manageable steps, making it easier to understand and solve problems. In this article, we will explore five ways to multiply using expanded form easily.

What is Expanded Form Multiplication?

Expanded form multiplication is a method of multiplying numbers by breaking them down into their place values. Each digit in the multiplicand is multiplied by the multiplier, and the results are added together to get the final product. This method is particularly useful when multiplying large numbers, as it helps to avoid mistakes and makes the calculation process more transparent.

Benefits of Using Expanded Form Multiplication

Using expanded form multiplication has several benefits, including:

• Improved accuracy: By breaking down the multiplication process into smaller steps, expanded form multiplication reduces the likelihood of errors.
• Enhanced understanding: This method helps students understand the concept of place value and how it applies to multiplication.
• Increased flexibility: Expanded form multiplication can be used to multiply numbers of varying sizes and complexities.

5 Ways to Multiply Using Expanded Form Easily

Here are five ways to multiply using expanded form easily:

1. Single-Digit Multiplication

Single-digit multiplication is the simplest form of expanded form multiplication. It involves multiplying a single-digit number by a multi-digit number.

Example: 4 × 23

= (4 × 20) + (4 × 3) = 80 + 12 = 92

Step-by-Step Process

1. Write the multiplicand (23) in expanded form: 20 + 3
2. Multiply the multiplier (4) by each part of the multiplicand: (4 × 20) + (4 × 3)
3. Calculate the products: 80 + 12
4. Add the products together: 92

2. Multi-Digit Multiplication

Multi-digit multiplication involves multiplying two multi-digit numbers using expanded form.

Example: 43 × 27

= (40 × 20) + (40 × 7) + (3 × 20) + (3 × 7) = 800 + 280 + 60 + 21 = 1161

Step-by-Step Process

1. Write both numbers in expanded form: 40 + 3 and 20 + 7
2. Multiply each part of one number by each part of the other number: (40 × 20) + (40 × 7) + (3 × 20) + (3 × 7)
3. Calculate the products: 800 + 280 + 60 + 21
4. Add the products together: 1161

3. Using Arrays

Arrays are a visual representation of multiplication, where the multiplicand is represented as an array of dots or blocks.

Example: 3 × 24

= (3 × 20) + (3 × 4)

4. Using the Distributive Property

The distributive property states that multiplication can be distributed over addition.

Example: 5 × (3 + 2)

= (5 × 3) + (5 × 2) = 15 + 10 = 25

Step-by-Step Process

1. Apply the distributive property: (5 × 3) + (5 × 2)
2. Calculate the products: 15 + 10
3. Add the products together: 25

5. Using Mental Math

Mental math involves performing calculations in your head without using paper or pencil.

Example: 6 × 9

= (6 × 10) - (6 × 1) = 60 - 6 = 54

Step-by-Step Process

1. Break down the multiplicand (9) into 10 - 1
2. Multiply the multiplier (6) by each part of the multiplicand: (6 × 10) - (6 × 1)
3. Calculate the products: 60 - 6
4. Subtract the products: 54

Conclusion

Multiplying numbers using expanded form is a valuable skill in mathematics. By breaking down the multiplication process into smaller steps, expanded form multiplication helps to improve accuracy, enhance understanding, and increase flexibility. The five methods outlined in this article provide a comprehensive approach to multiplying numbers using expanded form easily.

We hope you found this article informative and helpful. If you have any questions or comments, please feel free to share them below.