Magnitude Angle Form: Simplifying Complex Numbers

Quick Links :

Complex numbers have been a cornerstone of mathematics and physics for centuries, allowing us to represent and analyze phenomena that cannot be captured by real numbers alone. One of the most powerful ways to represent complex numbers is in magnitude angle form, also known as polar form. This representation offers a unique perspective on complex numbers, simplifying many calculations and providing insights into the nature of complex arithmetic.

In this article, we will delve into the world of magnitude angle form, exploring its definition, benefits, and applications. We will also examine the geometric interpretation of complex numbers in polar form and provide practical examples to illustrate its usefulness.

What is Magnitude Angle Form?

Magnitude angle form is a way to represent complex numbers in terms of their magnitude (or length) and angle. It is defined as follows:

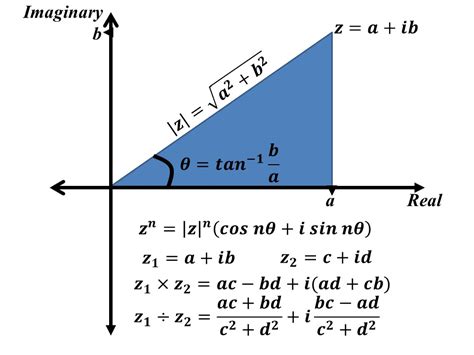
z = r(cos(θ) + i sin(θ))

where z is the complex number, r is the magnitude (or length), θ is the angle, and i is the imaginary unit.

In this representation, the magnitude r is a non-negative real number that represents the distance from the origin to the point in the complex plane. The angle θ is a real number that represents the direction from the positive real axis to the line connecting the origin to the point.

Why Use Magnitude Angle Form?

So, why would we want to use magnitude angle form instead of the more familiar Cartesian form (a + bi)? There are several reasons:

• Simplifies complex arithmetic: Many complex arithmetic operations, such as multiplication and division, are much simpler in polar form.
• Provides geometric insights: The polar form representation offers a clear geometric interpretation of complex numbers, making it easier to visualize and understand their behavior.
• Facilitates calculations: Polar form can simplify many calculations, such as finding the roots of complex numbers or calculating complex powers.

Geometric Interpretation of Complex Numbers

The geometric interpretation of complex numbers is a powerful tool for understanding their behavior. In the complex plane, each point corresponds to a complex number. The x-axis represents the real part, while the y-axis represents the imaginary part.

Using the polar form representation, we can visualize complex numbers as vectors in the complex plane. The magnitude r represents the length of the vector, while the angle θ represents the direction.

Applications of Magnitude Angle Form

Magnitude angle form has numerous applications in mathematics, physics, and engineering. Some examples include:

• Signal processing: Polar form is used extensively in signal processing to represent and analyze signals.
• Control systems: Polar form is used to analyze and design control systems, such as those used in robotics and aerospace engineering.
• Electrical engineering: Polar form is used to analyze and design electrical circuits, including filters and amplifiers.

Converting Between Cartesian and Polar Form

Converting between Cartesian and polar form is a straightforward process. To convert from Cartesian to polar form, we use the following formulas:

r = √(a^2 + b^2) θ = arctan(b/a)

where a and b are the real and imaginary parts of the complex number, respectively.

To convert from polar to Cartesian form, we use the following formulas:

a = r cos(θ) b = r sin(θ)

Examples and Exercises

Here are some examples to illustrate the use of magnitude angle form:

• Example 1: Find the polar form of the complex number 3 + 4i.
• Example 2: Find the Cartesian form of the complex number 2(cos(30°) + i sin(30°)).
• Exercise 1: Convert the complex number 5 + 12i to polar form.
• Exercise 2: Convert the complex number 2(cos(45°) + i sin(45°)) to Cartesian form.

Conclusion and Next Steps

In conclusion, magnitude angle form is a powerful tool for representing and analyzing complex numbers. Its geometric interpretation and simplification of complex arithmetic make it an essential part of any complex analysis toolkit.

We hope this article has provided a comprehensive introduction to magnitude angle form and its applications. For further reading, we recommend exploring the topics of complex analysis, signal processing, and control systems.

We encourage you to share your thoughts and feedback on this article in the comments below. If you have any questions or would like to discuss further, please don't hesitate to reach out.