Convert To Vertex Form: Simplify Intercept Form Equations

Quick Links :

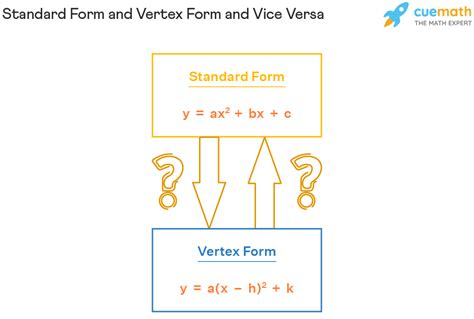
Converting equations from one form to another is a fundamental skill in algebra, and understanding how to simplify intercept form equations to vertex form can be incredibly useful. In this article, we will delve into the world of algebra, exploring the importance of converting equations between forms, the benefits of working with vertex form, and providing a step-by-step guide on how to convert intercept form equations to vertex form.

Why Convert Equations?

Converting equations from one form to another allows us to gain a deeper understanding of the underlying mathematical structure. Different forms can reveal distinct characteristics of the equation, making it easier to analyze and solve problems. In the case of quadratic equations, converting from intercept form to vertex form provides valuable insights into the graph's shape, orientation, and key features.

What is Vertex Form?

Vertex form is a way of expressing quadratic equations in the form y = a(x-h)^2 + k, where (h, k) represents the coordinates of the vertex. This form is particularly useful when working with parabolas, as it provides immediate information about the graph's vertex, axis of symmetry, and direction of opening.

Benefits of Vertex Form

Working with vertex form offers several benefits, including:

• Easy identification of vertex: The vertex form equation explicitly provides the coordinates of the vertex, making it simple to locate this critical point on the graph.

• Axis of symmetry: The axis of symmetry is easily identifiable in vertex form, as it passes through the vertex and is perpendicular to the directrix.

• Direction of opening: The coefficient a in vertex form determines the direction of opening, allowing us to quickly ascertain whether the parabola opens upwards or downwards.

How to Convert Intercept Form to Vertex Form

To convert an intercept form equation to vertex form, follow these steps:

1. Write the intercept form equation: Start by writing the given intercept form equation, typically in the form y = ax^2 + bx + c.

2. Complete the square: To convert the equation to vertex form, we need to complete the square. Begin by factoring out the coefficient a from the first two terms: y = a(x^2 + bx).

3. Find the value to complete the square: Calculate the value to complete the square by taking half of the coefficient b and squaring it: (-b/2)^2.

4. Add and subtract the value: Add and subtract the value calculated in step 3 inside the parentheses: y = a(x^2 + bx + (-b/2)^2 - (-b/2)^2).

5. Simplify and write in vertex form: Simplify the expression and rewrite it in vertex form: y = a(x - h)^2 + k, where h = -b/2a and k = c - (b^2/4a).

Example: Convert Intercept Form to Vertex Form

Suppose we want to convert the intercept form equation y = 2x^2 + 4x + 3 to vertex form.

1. Write the intercept form equation: y = 2x^2 + 4x + 3.

2. Complete the square: y = 2(x^2 + 2x).

3. Find the value to complete the square: (-2/2)^2 = 1.

4. Add and subtract the value: y = 2(x^2 + 2x + 1 - 1).

5. Simplify and write in vertex form: y = 2(x + 1)^2 - 1.

Practical Applications

Converting intercept form equations to vertex form has numerous practical applications in fields such as physics, engineering, and computer science. For instance, understanding the vertex form of a parabola can help us:

• Model real-world phenomena: Vertex form can be used to model the trajectory of projectiles, the shape of satellite dishes, and the curvature of mirrors.

• Analyze and solve problems: By converting equations to vertex form, we can gain valuable insights into the underlying mathematical structure, making it easier to analyze and solve problems.

• Make predictions and estimates: The vertex form of a parabola provides immediate information about the graph's shape and orientation, allowing us to make predictions and estimates about real-world phenomena.

Conclusion and Call to Action

In this article, we explored the importance of converting equations from intercept form to vertex form, highlighting the benefits of working with vertex form and providing a step-by-step guide on how to make the conversion. Whether you're a student, teacher, or professional, mastering this skill can have a significant impact on your understanding and analysis of quadratic equations.

Take the next step by practicing the conversion process with different intercept form equations. Share your experiences, ask questions, and explore the various applications of vertex form in different fields. Together, let's delve deeper into the world of algebra and uncover the secrets hidden within these powerful equations.