Mastering Slope Intercept Form: A Comprehensive Guide

Linear equations are a fundamental concept in mathematics, and one of the most commonly used forms is the slope-intercept form. It's a powerful tool for solving equations, graphing lines, and understanding the relationships between variables. In this article, we'll delve into the world of slope-intercept form, exploring its definition, benefits, and applications. By the end of this guide, you'll be well-versed in using slope-intercept form to tackle even the most complex equations.
What is Slope Intercept Form?
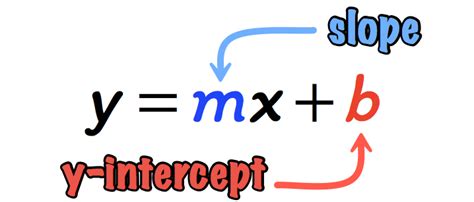
The slope-intercept form of a linear equation is a way of expressing the equation in a specific format, which makes it easier to work with. It's defined as:
y = mx + b
where:
- y is the dependent variable (the variable being measured)
- m is the slope (the rate of change of the line)
- x is the independent variable (the variable being changed)
- b is the y-intercept (the point where the line crosses the y-axis)
This form is particularly useful because it allows you to quickly identify the slope and y-intercept of a line, which are essential components of linear equations.
Benefits of Slope Intercept Form

So, why is slope-intercept form so important? Here are just a few benefits:
- Easy to graph: With the slope and y-intercept readily available, you can quickly graph a line using the slope-intercept form.
- Simple to solve: Slope-intercept form makes it easy to solve for y, as you can simply plug in the value of x and calculate the corresponding y-value.
- Useful for modeling: Slope-intercept form is commonly used in real-world applications, such as physics, engineering, and economics, to model relationships between variables.
How to Convert to Slope Intercept Form
Converting an equation to slope-intercept form is a straightforward process. Here are the steps:
- Start with a linear equation: Begin with a linear equation in any form, such as standard form (ax + by = c) or point-slope form (y - y1 = m(x - x1)).
- Isolate y: Rearrange the equation to isolate y on one side of the equation.
- Simplify the equation: Combine like terms and simplify the equation to put it in slope-intercept form.
Example Problems

Let's work through a few example problems to illustrate the process:
Problem 1: Convert the equation 2x + 3y = 7 to slope-intercept form.
Solution:
- Isolate y: 3y = -2x + 7
- Simplify: y = (-2/3)x + 7/3
Problem 2: Convert the equation x - 2y = -3 to slope-intercept form.
Solution:
- Isolate y: -2y = -x - 3
- Simplify: y = (1/2)x + 3/2
Real-World Applications
Slope-intercept form has numerous real-world applications, including:
- Physics: Slope-intercept form is used to model the motion of objects, including the trajectory of projectiles and the force of friction.
- Economics: Slope-intercept form is used to model the relationships between economic variables, such as supply and demand curves.
- Engineering: Slope-intercept form is used to design and optimize systems, including electrical circuits and mechanical systems.
Conclusion
Slope-intercept form is a powerful tool for working with linear equations. By mastering this form, you'll be able to quickly solve equations, graph lines, and model real-world relationships. Remember, the key to success lies in understanding the benefits and applications of slope-intercept form.
What is the difference between slope-intercept form and standard form?
+Slope-intercept form (y = mx + b) and standard form (ax + by = c) are two different ways of expressing a linear equation. Slope-intercept form is more useful for graphing and solving for y, while standard form is more useful for finding the x-intercept and solving for x.
How do I find the slope and y-intercept of a line?
+The slope (m) can be found using the formula m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line. The y-intercept (b) can be found by plugging in the value of x and solving for y.
What are some common mistakes to avoid when working with slope-intercept form?
+Common mistakes include forgetting to isolate y, simplifying the equation incorrectly, and failing to check the solution. It's also important to ensure that the equation is in the correct form before attempting to solve or graph it.
We hope this comprehensive guide has helped you master slope-intercept form. Do you have any questions or need further clarification? Share your thoughts in the comments below!