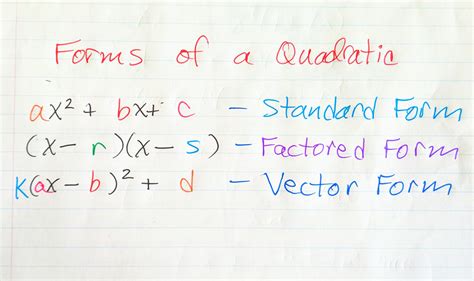5 Easy Steps To Standard Quadratic Form

Quick Links :

Converting a quadratic equation to standard form is a crucial step in solving quadratic equations. A quadratic equation in standard form is written in the format ax^2 + bx + c = 0, where a, b, and c are constants. In this article, we will explore the 5 easy steps to convert a quadratic equation to standard quadratic form.

Understanding the Importance of Standard Quadratic Form

Converting a quadratic equation to standard form is essential in solving quadratic equations. It helps in identifying the coefficients of the quadratic equation, which are necessary for factoring, solving, and graphing. Moreover, standard form makes it easier to compare and contrast different quadratic equations.

The Benefits of Standard Quadratic Form

Standard quadratic form offers several benefits, including:

• Easy identification of coefficients
• Simplified factoring and solving
• Enhanced graphing capabilities
• Improved comparison and contrast of quadratic equations

Step 1: Identify the Quadratic Equation

The first step in converting a quadratic equation to standard form is to identify the quadratic equation. This involves reading the problem and understanding the given quadratic equation. The quadratic equation may be given in various forms, such as:

• Factored form: (x + 2)(x - 3) = 0
• Vertex form: y = a(x - h)^2 + k
• General form: ax^2 + bx + c = 0

Example: Identify the Quadratic Equation

Suppose we are given the quadratic equation: x^2 + 5x + 6 = 0

In this example, the quadratic equation is already in general form.

Step 2: Expand the Quadratic Equation (If Necessary)

If the quadratic equation is given in factored form or vertex form, we need to expand it to convert it to standard form. This involves multiplying the factors or expanding the squared term.

Example: Expand the Quadratic Equation

Suppose we are given the quadratic equation: (x + 2)(x - 3) = 0

To expand this equation, we multiply the factors:

x^2 - 3x + 2x - 6 = 0

x^2 - x - 6 = 0

Step 3: Simplify the Quadratic Equation

After expanding the quadratic equation (if necessary), we need to simplify it by combining like terms. This involves adding or subtracting the coefficients of the same variable.

Example: Simplify the Quadratic Equation

Suppose we are given the quadratic equation: x^2 - x - 6 = 0

This equation is already simplified.

Step 4: Rearrange the Quadratic Equation

If the quadratic equation is not in the standard form ax^2 + bx + c = 0, we need to rearrange it. This involves moving the constant term to the right-hand side of the equation.

Example: Rearrange the Quadratic Equation

Suppose we are given the quadratic equation: x^2 - x - 6 = 0

To rearrange this equation, we move the constant term to the right-hand side:

x^2 - x = 6

Step 5: Write the Quadratic Equation in Standard Form

The final step is to write the quadratic equation in standard form. This involves ensuring that the equation is in the format ax^2 + bx + c = 0.

Example: Write the Quadratic Equation in Standard Form

Suppose we are given the quadratic equation: x^2 - x - 6 = 0

This equation is already in standard form.

By following these 5 easy steps, you can convert any quadratic equation to standard quadratic form.

Conclusion: Mastering Standard Quadratic Form

Mastering standard quadratic form is essential for solving quadratic equations. By following the 5 easy steps outlined in this article, you can convert any quadratic equation to standard form and solve it with ease. Remember to practice regularly to reinforce your understanding of standard quadratic form.

We hope this article has helped you understand the importance of standard quadratic form and how to convert a quadratic equation to standard form. If you have any questions or need further clarification, please don't hesitate to ask.

FAQ Section: