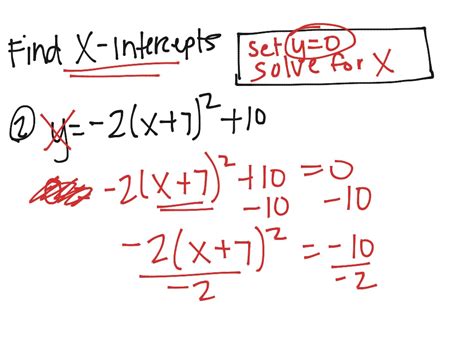3 Ways To Find X Intercepts From Vertex Form

Quick Links :

Finding the x-intercepts of a quadratic function is an essential skill in algebra, and it can be particularly useful when working with vertex form. The vertex form of a quadratic function is given by y = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola. In this article, we will explore three methods to find the x-intercepts of a quadratic function in vertex form.

Method 1: Factoring the Vertex Form

One way to find the x-intercepts of a quadratic function in vertex form is by factoring the expression. To factor the vertex form, we need to rewrite it as y = a(x - h)(x - h) + k. This allows us to easily identify the x-intercepts, which occur when the expression inside the parentheses equals zero.

For example, consider the quadratic function y = 2(x - 3)^2 + 4. To factor this expression, we can rewrite it as y = 2(x - 3)(x - 3) + 4. Setting the expression inside the parentheses equal to zero gives us x - 3 = 0, which yields x = 3. Therefore, the x-intercept of this quadratic function is x = 3.

Step-by-Step Instructions:

• Rewrite the vertex form as y = a(x - h)(x - h) + k.
• Set the expression inside the parentheses equal to zero.
• Solve for x.

Method 2: Using the Quadratic Formula

Another way to find the x-intercepts of a quadratic function in vertex form is by using the quadratic formula. The quadratic formula states that for a quadratic function in the form ax^2 + bx + c, the x-intercepts can be found using the formula x = (-b ± √(b^2 - 4ac)) / 2a.

To apply this formula to a quadratic function in vertex form, we need to rewrite it in the standard form ax^2 + bx + c. This involves expanding the vertex form and combining like terms.

For example, consider the quadratic function y = 3(x - 2)^2 + 5. To rewrite this expression in standard form, we can expand it as y = 3(x^2 - 4x + 4) + 5, which simplifies to y = 3x^2 - 12x + 17. Using the quadratic formula, we can now find the x-intercepts of this function.

Step-by-Step Instructions:

• Rewrite the vertex form in standard form ax^2 + bx + c.
• Apply the quadratic formula to find the x-intercepts.

Method 3: Graphing the Parabola

A third method to find the x-intercepts of a quadratic function in vertex form is by graphing the parabola. This involves plotting the vertex and several other points on the graph to determine the shape of the parabola.

To graph a quadratic function in vertex form, we can start by plotting the vertex (h, k). We can then use the symmetry of the parabola to plot other points on the graph. Finally, we can draw a smooth curve through the points to create the parabola.

For example, consider the quadratic function y = 2(x - 1)^2 + 3. To graph this function, we can start by plotting the vertex (1, 3). We can then use the symmetry of the parabola to plot other points on the graph, such as (0, 5) and (2, 5). Finally, we can draw a smooth curve through the points to create the parabola.

Step-by-Step Instructions:

• Plot the vertex (h, k) on the graph.
• Use the symmetry of the parabola to plot other points on the graph.
• Draw a smooth curve through the points to create the parabola.

In conclusion, there are several methods to find the x-intercepts of a quadratic function in vertex form. Whether you choose to factor the vertex form, use the quadratic formula, or graph the parabola, each method can be an effective way to find the x-intercepts of a quadratic function.

Now it's your turn! Take a moment to practice finding the x-intercepts of a quadratic function in vertex form using one of the methods described above. Share your results in the comments below, and don't hesitate to ask for help if you need it.