Find Slope Intercept Form With Two Points Easily

Quick Links :

The slope-intercept form of a linear equation is one of the most widely used forms in mathematics and real-world applications. It provides a clear and concise way to express the relationship between two variables. If you're given two points on a line, finding the slope-intercept form can seem like a daunting task. However, with the right steps and a little practice, you'll be able to find the slope-intercept form with ease.

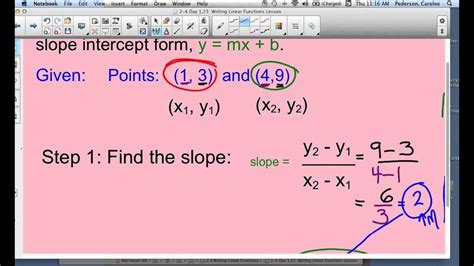
To begin, let's recall the slope-intercept form of a linear equation: y = mx + b, where m represents the slope and b represents the y-intercept. The slope indicates the rate of change between the two variables, while the y-intercept is the point at which the line crosses the y-axis.

Given two points on a line, you can find the slope using the formula: m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of the two points. This formula calculates the rate of change between the two points.

Step-by-Step Guide to Finding Slope-Intercept Form

Now, let's walk through a step-by-step guide on how to find the slope-intercept form using two points.

Step 1: Identify the Two Points

Identify the coordinates of the two points on the line. Let's say the two points are (2, 3) and (4, 5).

Step 2: Calculate the Slope

Using the slope formula, calculate the slope (m) using the coordinates of the two points: m = (5 - 3) / (4 - 2) = 2 / 2 = 1.

Step 3: Use One of the Points to Find the Y-Intercept

Now that you have the slope (m = 1), use one of the points to find the y-intercept (b). Let's use the point (2, 3). Plug in the values into the slope-intercept form: 3 = 1(2) + b. Solve for b: b = 3 - 2 = 1.

Step 4: Write the Slope-Intercept Form

With the slope (m = 1) and y-intercept (b = 1), write the slope-intercept form of the linear equation: y = x + 1.

Example Problems

Let's practice finding the slope-intercept form using two points with a few example problems.

Example 1

Find the slope-intercept form of the line that passes through the points (1, 2) and (3, 4).

Solution: m = (4 - 2) / (3 - 1) = 2 / 2 = 1 Using the point (1, 2): 2 = 1(1) + b, b = 2 - 1 = 1 Slope-intercept form: y = x + 1

Example 2

Find the slope-intercept form of the line that passes through the points (-2, 3) and (1, 5).

Solution: m = (5 - 3) / (1 - (-2)) = 2 / 3 Using the point (-2, 3): 3 = (2/3)(-2) + b, b = 3 + 4/3 = 13/3 Slope-intercept form: y = (2/3)x + 13/3

Benefits of Finding Slope-Intercept Form

Finding the slope-intercept form of a linear equation has numerous benefits in mathematics and real-world applications.

Easier Graphing

The slope-intercept form makes it easier to graph linear equations. With the slope and y-intercept, you can quickly identify the line's direction and position on the coordinate plane.

Real-World Applications

The slope-intercept form is widely used in various real-world applications, such as physics, engineering, and economics. It helps model real-world phenomena, make predictions, and analyze data.

Simplifies Calculations

The slope-intercept form simplifies calculations involving linear equations. It provides a clear and concise way to express the relationship between two variables, making it easier to perform calculations and solve problems.

Conclusion

Finding the slope-intercept form of a linear equation using two points is a straightforward process. By following the step-by-step guide and practicing with example problems, you'll become proficient in finding the slope-intercept form with ease. Remember to identify the two points, calculate the slope, use one of the points to find the y-intercept, and write the slope-intercept form. With its numerous benefits in mathematics and real-world applications, finding the slope-intercept form is an essential skill to master.

Get Involved

Now that you've learned how to find the slope-intercept form using two points, it's time to practice and apply your knowledge. Try solving example problems and exploring real-world applications that involve linear equations. Share your thoughts and questions in the comments section below. Don't forget to like and share this article with your friends and colleagues who may find it helpful.