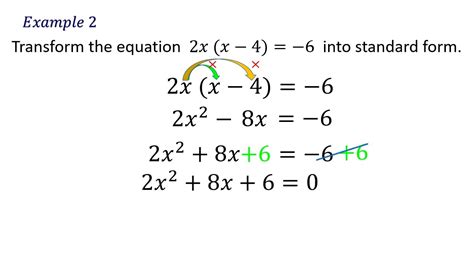Write A Quadratic Function In Standard Form Easily

Quick Links :

Hide

Understanding quadratic functions is crucial in mathematics, particularly in algebra and calculus. A quadratic function in standard form is expressed as f(x) = ax^2 + bx + c, where 'a', 'b', and 'c' are constants, and 'a' cannot be zero. This form is useful for identifying the vertex, axis of symmetry, and the direction of the parabola's opening.

Why is Standard Form Important?

Writing a quadratic function in standard form is essential because it allows us to easily identify key characteristics of the parabola it represents. The standard form provides a straightforward way to determine the vertex, axis of symmetry, and the direction of the parabola's opening, which is crucial in solving problems related to quadratic equations.

Identifying Key Components

• The coefficient 'a' determines the direction and width of the parabola. If 'a' is positive, the parabola opens upwards; if 'a' is negative, it opens downwards. The larger the absolute value of 'a', the narrower the parabola.
• The coefficient 'b' affects the position of the axis of symmetry and the vertex of the parabola.
• The constant 'c' represents the y-intercept, which is the point where the parabola intersects the y-axis.

Steps to Write a Quadratic Function in Standard Form

Converting a quadratic function to standard form involves rearranging the terms to ensure the squared variable term comes first, followed by the linear term, and then the constant term.

Step 1: Identify the Squared Variable Term

Start by identifying the term with the squared variable. This term should be the first term in the standard form.

Step 2: Identify the Linear Term

Next, identify the term with the variable raised to the power of one. This term should be the second term in the standard form.

Step 3: Identify the Constant Term

Finally, identify the constant term, which is the term without any variable. This term should be the last term in the standard form.

Step 4: Rearrange the Terms

Rearrange the terms to ensure the squared variable term comes first, followed by the linear term, and then the constant term.

Example

Suppose we have the quadratic function f(x) = 2x + 3x^2 - 4. To write this function in standard form, we need to rearrange the terms:

f(x) = 3x^2 + 2x - 4

This quadratic function is now in standard form, with the squared variable term first, followed by the linear term, and then the constant term.

Benefits of Standard Form

Writing a quadratic function in standard form provides several benefits:

• Easy Identification of Key Components: The standard form allows us to easily identify the vertex, axis of symmetry, and the direction of the parabola's opening.
• Simplifies Problem-Solving: The standard form simplifies the process of solving quadratic equations and inequalities.
• Facilitates Graphing: The standard form makes it easier to graph quadratic functions by providing a clear understanding of the parabola's shape and position.

Common Applications of Standard Form

The standard form of a quadratic function has numerous applications in various fields, including:

• Physics and Engineering: Quadratic functions are used to model the motion of objects, including the trajectory of projectiles and the vibration of springs.
• Economics: Quadratic functions are used to model the relationship between price and demand, as well as the cost of production.
• Computer Science: Quadratic functions are used in algorithms for solving optimization problems.

Conclusion

Writing a quadratic function in standard form is a crucial skill in mathematics and has numerous applications in various fields. By following the steps outlined above, you can easily convert a quadratic function to standard form and gain a deeper understanding of the parabola it represents.

Now, it's your turn! Share your thoughts and experiences with writing quadratic functions in standard form. Do you have any tips or tricks to share? Leave a comment below and let's get the conversation started!