5 Ways To Master Graphing Quadratic Functions Vertex Form

Quick Links :

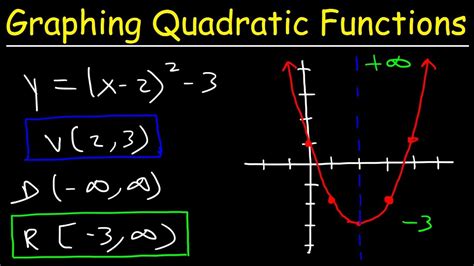
Mastering graphing quadratic functions in vertex form is a crucial skill for any student of mathematics, particularly those in high school or introductory college algebra courses. Quadratic functions in vertex form provide a unique way of representing parabolas, allowing for the identification of key features such as the vertex, axis of symmetry, and the direction of the parabola's opening. In this article, we will explore five ways to master graphing quadratic functions in vertex form, along with practical examples and explanations.

Understanding the Basics of Quadratic Functions in Vertex Form

Quadratic functions in vertex form are written in the form f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola, and a determines the direction and width of the parabola's opening. Understanding the role of each component is essential for graphing these functions accurately.

Components of the Vertex Form

• a: This coefficient determines the direction and width of the parabola's opening. If a > 0, the parabola opens upwards; if a < 0, it opens downwards. The larger the absolute value of a, the narrower the parabola.
• (h, k): The vertex of the parabola, where h represents the x-coordinate and k the y-coordinate.

Method 1: Identify the Vertex and Determine the Direction

The first step in graphing a quadratic function in vertex form is to identify the vertex (h, k) and determine the direction of the parabola based on the value of a. If a is positive, the parabola opens upwards; if a is negative, it opens downwards.

Example: Graph `f(x) = 2(x - 3)^2 + 1`

• Identify the vertex: (h, k) = (3, 1)
• Determine the direction: Since a = 2, which is positive, the parabola opens upwards.

Method 2: Plot Key Points

After identifying the vertex and determining the direction, plot key points on either side of the vertex to begin sketching the parabola. This can include the x-intercepts (if a is positive) or the points where the parabola intersects the y-axis (if a is negative).

Example: Continue with `f(x) = 2(x - 3)^2 + 1`

• Plot key points: Since the vertex is (3, 1), plot points at x = 2 and x = 4 to sketch the parabola.

Method 3: Use the Axis of Symmetry

The axis of symmetry is a vertical line that passes through the vertex and is symmetric with respect to the parabola. The equation of the axis of symmetry is x = h, where h is the x-coordinate of the vertex.

Example: Continue with `f(x) = 2(x - 3)^2 + 1`

• Use the axis of symmetry: Since the vertex is (3, 1), the axis of symmetry is x = 3.

Method 4: Identify the X-Intercepts (If Applicable)

If the parabola opens upwards (i.e., a > 0), the x-intercepts can be found by setting f(x) = 0 and solving for x. This can help in sketching the parabola.

Example: Continue with `f(x) = 2(x - 3)^2 + 1`

• Identify the x-intercepts: Since the parabola opens upwards, set f(x) = 0 and solve for x to find the x-intercepts.

Method 5: Sketch the Parabola

Using the vertex, direction, key points, axis of symmetry, and x-intercepts (if applicable), sketch the parabola. Make sure to label the vertex, axis of symmetry, and x-intercepts.

Example: Continue with `f(x) = 2(x - 3)^2 + 1`

• Sketch the parabola: Using the vertex (3, 1), direction (upwards), key points, axis of symmetry x = 3, and x-intercepts, sketch the parabola.

By mastering these five methods, you will become proficient in graphing quadratic functions in vertex form. Remember to identify the vertex and determine the direction, plot key points, use the axis of symmetry, identify the x-intercepts (if applicable), and sketch the parabola.

Now, we invite you to share your thoughts on graphing quadratic functions in vertex form. Have you encountered any challenges while graphing these functions? Share your experiences and questions in the comments below. Don't forget to share this article with your friends and classmates who might find it helpful.