5 Ways To Express Forces In Cartesian Vector Form

Quick Links :

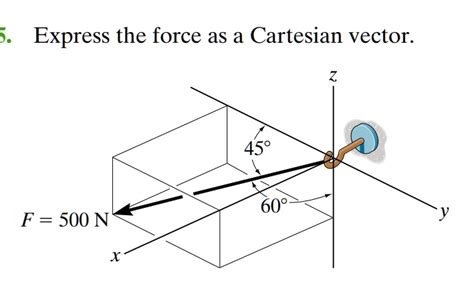
Forces are a fundamental concept in physics and engineering, and expressing them in Cartesian vector form is a crucial skill for any student or professional in these fields. Cartesian vector form is a mathematical way of representing forces and other quantities in three-dimensional space, using the x, y, and z axes. In this article, we will explore five ways to express forces in Cartesian vector form, including the use of unit vectors, magnitude and direction, components, scalar multiplication, and vector addition.

Understanding Cartesian Vector Form

Before we dive into the five ways to express forces in Cartesian vector form, let's take a moment to understand the basics of Cartesian vector form. In Cartesian vector form, a force is represented as a vector with both magnitude (amount of movement) and direction. The vector is typically represented in three-dimensional space, using the x, y, and z axes. The force vector can be represented using unit vectors, which are vectors with a magnitude of 1 and direction along the x, y, or z axes.

1. Using Unit Vectors

One way to express a force in Cartesian vector form is to use unit vectors. Unit vectors are vectors with a magnitude of 1 and direction along the x, y, or z axes. To represent a force using unit vectors, we multiply the unit vector by the magnitude of the force in that direction. For example, if we have a force F = 5 N in the x-direction, we can represent it as F = 5i, where i is the unit vector in the x-direction.

Example: Representing a Force Using Unit Vectors

Suppose we have a force F = 10 N at an angle of 30° from the x-axis. We can represent this force using unit vectors as follows:

F = 10i + 5j

where i is the unit vector in the x-direction and j is the unit vector in the y-direction.

2. Magnitude and Direction

Another way to express a force in Cartesian vector form is to specify its magnitude and direction. The magnitude of a force is its amount of movement, while the direction is the angle it makes with the x-axis. To represent a force using magnitude and direction, we use the formula:

F = |F|cosθi + |F|sinθj

where |F| is the magnitude of the force and θ is the angle it makes with the x-axis.

Example: Representing a Force Using Magnitude and Direction

Suppose we have a force F = 20 N at an angle of 45° from the x-axis. We can represent this force using magnitude and direction as follows:

F = 20cos(45)i + 20sin(45)j

3. Components

A third way to express a force in Cartesian vector form is to specify its components along the x, y, and z axes. The components of a force are the amounts of movement in each direction. To represent a force using components, we use the formula:

F = Fxi + Fyj + Fzk

where Fx, Fy, and Fz are the components of the force along the x, y, and z axes, respectively.

Example: Representing a Force Using Components

Suppose we have a force F = 15 N with components Fx = 10 N, Fy = 5 N, and Fz = 0 N. We can represent this force using components as follows:

F = 10i + 5j + 0k

4. Scalar Multiplication

A fourth way to express a force in Cartesian vector form is to use scalar multiplication. Scalar multiplication is the process of multiplying a vector by a scalar (a number) to change its magnitude. To represent a force using scalar multiplication, we multiply the force vector by a scalar.

Example: Representing a Force Using Scalar Multiplication

Suppose we have a force F = 10 N in the x-direction. We can represent this force using scalar multiplication as follows:

F = 2(5i) = 10i

5. Vector Addition

A fifth way to express a force in Cartesian vector form is to use vector addition. Vector addition is the process of adding two or more vectors to find the resultant vector. To represent a force using vector addition, we add the force vectors.

Example: Representing a Force Using Vector Addition

Suppose we have two forces, F1 = 10 N in the x-direction and F2 = 5 N in the y-direction. We can represent the resultant force using vector addition as follows:

F = F1 + F2 = 10i + 5j

In conclusion, expressing forces in Cartesian vector form is a fundamental skill in physics and engineering. We have explored five ways to express forces in Cartesian vector form, including using unit vectors, magnitude and direction, components, scalar multiplication, and vector addition. By mastering these techniques, you can become proficient in representing forces in Cartesian vector form and solve problems in physics and engineering with ease.

We hope this article has been informative and helpful. Please feel free to comment or share this article with your friends and colleagues. If you have any questions or need further clarification on any of the topics discussed, please don't hesitate to ask.