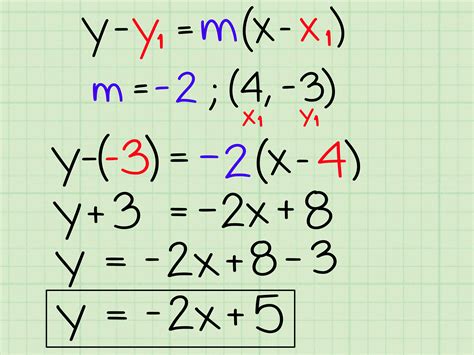Mastering Slope Intercept Form In 5 Easy Steps

Quick Links :

Slope intercept form is a fundamental concept in algebra and geometry, and it's used to describe the equation of a line in a two-dimensional coordinate system. Understanding this concept is crucial for solving problems in various mathematical and scientific fields, from simple graphing to complex calculations. In this article, we'll break down the slope intercept form into 5 easy-to-follow steps, making it accessible to anyone who wants to master this essential mathematical concept.

The importance of slope intercept form lies in its ability to provide a clear and concise way of expressing the equation of a line. It's used in various real-world applications, such as physics, engineering, economics, and computer science. By mastering slope intercept form, you'll be able to tackle complex problems with confidence and accuracy. So, let's dive into the world of slope intercept form and explore its 5 easy steps.

Step 1: Understand the Basics of Slope Intercept Form

The slope intercept form is represented by the equation y = mx + b, where:

• y is the dependent variable (the y-coordinate of a point on the line)
• m is the slope of the line (a measure of how steep it is)
• x is the independent variable (the x-coordinate of a point on the line)
• b is the y-intercept (the point where the line intersects the y-axis)

In this step, it's essential to understand the relationship between the slope, y-intercept, and the equation of the line.

Key Takeaway:

• The slope intercept form is a linear equation that describes the relationship between the x and y variables.

Step 2: Find the Slope (m)

The slope (m) is a crucial component of the slope intercept form. It represents the rate of change of the line, and it's calculated using the formula:

m = (y2 - y1) / (x2 - x1)

where (x1, y1) and (x2, y2) are two points on the line.

To find the slope, you can use the following steps:

1. Choose two points on the line (x1, y1) and (x2, y2).
2. Calculate the difference in y-coordinates (y2 - y1).
3. Calculate the difference in x-coordinates (x2 - x1).
4. Divide the difference in y-coordinates by the difference in x-coordinates.

Example:

Find the slope of the line passing through points (2, 3) and (4, 5).

m = (5 - 3) / (4 - 2) = 2 / 2 = 1

Step 3: Find the Y-Intercept (b)

The y-intercept (b) is the point where the line intersects the y-axis. To find the y-intercept, you can use the following steps:

1. Choose a point on the line (x, y).
2. Substitute the x-coordinate into the equation y = mx + b.
3. Solve for b.

Example:

Find the y-intercept of the line passing through point (2, 3) with a slope of 1.

3 = 1(2) + b 3 = 2 + b b = 1

Step 4: Write the Equation in Slope Intercept Form

Now that you have the slope (m) and y-intercept (b), you can write the equation of the line in slope intercept form:

y = mx + b

Example:

Write the equation of the line passing through point (2, 3) with a slope of 1 and y-intercept of 1.

y = 1x + 1 y = x + 1

Step 5: Graph the Line

The final step is to graph the line using the equation in slope intercept form. You can use a graphing calculator or plot the points manually.

Example:

Graph the line y = x + 1.

To graph the line, plot the y-intercept (0, 1) and use the slope (1) to find another point on the line. For example, if you move 1 unit to the right, the y-coordinate increases by 1 unit.

By following these 5 easy steps, you can master the slope intercept form and solve problems with confidence.

We hope this article has helped you master the slope intercept form in 5 easy steps. Remember to practice regularly to reinforce your understanding of this essential mathematical concept. If you have any questions or need further clarification, feel free to comment below. Share this article with your friends and classmates to help them master the slope intercept form as well. Happy learning!