Graphing A Parabola From Vertex Form Made Easy

Quick Links :

Understanding the intricacies of parabolas and their graphical representations can be a daunting task for many. However, grasping the concept of vertex form can make graphing parabolas significantly easier. In this comprehensive guide, we will delve into the world of parabolas, explore the vertex form, and provide a step-by-step approach to graphing parabolas with ease.

The Importance of Parabolas in Mathematics and Real-Life Applications

Parabolas are ubiquitous in mathematics and real-life applications. They can be seen in the trajectories of projectiles, the shape of satellite dishes, and even the curves of roller coasters. Understanding parabolas is essential for problem-solving in various fields, including physics, engineering, and architecture. Moreover, graphing parabolas can help visualize complex relationships between variables, making it a valuable tool for data analysis and interpretation.

What is Vertex Form?

Vertex form is a way of expressing a quadratic function in the form y = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola. This form is particularly useful for graphing parabolas, as it provides essential information about the parabola's shape, size, and position.

Benefits of Vertex Form

Using vertex form offers several benefits when graphing parabolas:

• Easy identification of the vertex: The vertex form explicitly states the coordinates of the vertex, making it simple to plot the vertex on the graph. • Determination of the axis of symmetry: The axis of symmetry is a vertical line that passes through the vertex, and its equation can be easily determined from the vertex form. • Graphing the parabola: With the vertex and axis of symmetry identified, graphing the parabola becomes a straightforward process.

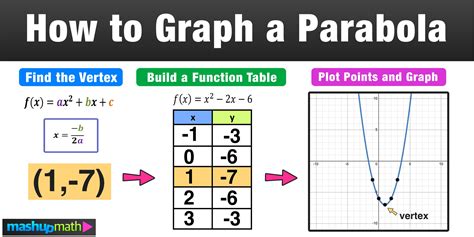
Step-by-Step Guide to Graphing a Parabola from Vertex Form

To graph a parabola from vertex form, follow these steps:

1. Identify the vertex: Extract the values of h and k from the vertex form, which represent the coordinates of the vertex.
2. Determine the axis of symmetry: The axis of symmetry is a vertical line that passes through the vertex, with the equation x = h.
3. Plot the vertex: Mark the vertex on the graph using the coordinates (h, k).
4. Plot additional points: Choose values for x and substitute them into the equation to find corresponding values for y. Plot these points on the graph.
5. Draw the parabola: Connect the plotted points with a smooth curve, ensuring that the parabola passes through the vertex and is symmetrical about the axis of symmetry.

Example: Graphing a Parabola from Vertex Form

Suppose we want to graph the parabola represented by the equation y = 2(x - 3)^2 + 1.

1. Identify the vertex: The vertex form gives us the values h = 3 and k = 1, which represent the coordinates of the vertex.
2. Determine the axis of symmetry: The axis of symmetry is a vertical line that passes through the vertex, with the equation x = 3.
3. Plot the vertex: Mark the vertex on the graph using the coordinates (3, 1).
4. Plot additional points: Choose values for x and substitute them into the equation to find corresponding values for y.
5. Draw the parabola: Connect the plotted points with a smooth curve, ensuring that the parabola passes through the vertex and is symmetrical about the axis of symmetry.

Practical Applications of Graphing Parabolas

Graphing parabolas has numerous practical applications in various fields, including:

• Physics and Engineering: Graphing parabolas is essential for modeling the trajectories of projectiles, designing roller coasters, and optimizing the shape of satellite dishes. • Data Analysis: Graphing parabolas can help visualize complex relationships between variables, making it a valuable tool for data analysis and interpretation. • Architecture: Graphing parabolas is used in architecture to design curved structures, such as bridges and arches.

Conclusion

Graphing parabolas from vertex form is a straightforward process that can be mastered with practice. By understanding the benefits of vertex form and following the step-by-step guide, you can easily graph parabolas and unlock a deeper understanding of quadratic functions. Whether you're a student, teacher, or professional, graphing parabolas is an essential skill that can be applied to various fields and real-life applications.

What do you think? Share your thoughts on graphing parabolas from vertex form in the comments below.

FAQ Section