Unlocking the Power of Derivatives: A Comprehensive Guide to Limit Form

Derivatives, a fundamental concept in calculus, play a crucial role in understanding the behavior of functions. The limit form of a derivative is a mathematical expression that describes the rate of change of a function at a specific point. In this article, we will explore five ways to understand derivatives in limit form, helping you grasp this complex concept and unlock the full potential of calculus.
As we delve into the world of derivatives, it's essential to understand the significance of limit form. The limit form of a derivative allows us to examine the rate of change of a function at a specific point, which is critical in various fields, such as physics, engineering, and economics. By mastering the limit form, you'll be able to analyze complex problems, make informed decisions, and drive innovation.
What are Derivatives in Limit Form?

A derivative in limit form is a mathematical expression that represents the rate of change of a function at a specific point. It's defined as the limit of the average rate of change of the function as the change in the input (or independent variable) approaches zero. In other words, it measures how fast the output (or dependent variable) changes when the input changes by a small amount.
Mathematically, the derivative of a function f(x) is represented as:
f'(x) = lim(h → 0) [f(x + h) - f(x)]/h
Where h is the change in the input, and the limit is taken as h approaches zero.
Method 1: Understanding the Concept of Limits

To understand derivatives in limit form, you need to grasp the concept of limits. A limit represents the value that a function approaches as the input gets arbitrarily close to a specific point. In the context of derivatives, the limit represents the rate of change of the function at that point.
To illustrate this concept, consider the function f(x) = x^2. As x approaches 2, the value of f(x) approaches 4. In this case, the limit of f(x) as x approaches 2 is 4.
Example: Finding the Limit of a Function
Find the limit of the function f(x) = 3x as x approaches 4.
Solution: As x approaches 4, the value of f(x) approaches 12.
Method 2: Visualizing the Derivative as a Slope

Another way to understand derivatives in limit form is to visualize the derivative as a slope. The derivative of a function at a point represents the slope of the tangent line to the graph of the function at that point.
Consider the function f(x) = x^2. The derivative of f(x) at x = 2 represents the slope of the tangent line to the graph of f(x) at the point (2, 4).
Example: Finding the Derivative as a Slope
Find the derivative of the function f(x) = 2x as x approaches 3.
Solution: The derivative of f(x) as x approaches 3 represents the slope of the tangent line to the graph of f(x) at the point (3, 6). The slope is 2.
Method 3: Using the Definition of a Derivative

You can also understand derivatives in limit form by using the definition of a derivative. The definition states that the derivative of a function f(x) is the limit of the average rate of change of the function as the change in the input approaches zero.
Consider the function f(x) = x^2. Using the definition, we can find the derivative of f(x) at x = 2 as follows:
f'(2) = lim(h → 0) [f(2 + h) - f(2)]/h = lim(h → 0) [(2 + h)^2 - 4]/h = lim(h → 0) [4 + 4h + h^2 - 4]/h = lim(h → 0) [4h + h^2]/h = lim(h → 0) [4 + h] = 4
Example: Finding the Derivative Using the Definition
Find the derivative of the function f(x) = 3x as x approaches 4.
Solution: Using the definition, we can find the derivative of f(x) at x = 4 as follows:
f'(4) = lim(h → 0) [f(4 + h) - f(4)]/h = lim(h → 0) [3(4 + h) - 12]/h = lim(h → 0) [12 + 3h - 12]/h = lim(h → 0) [3h]/h = 3
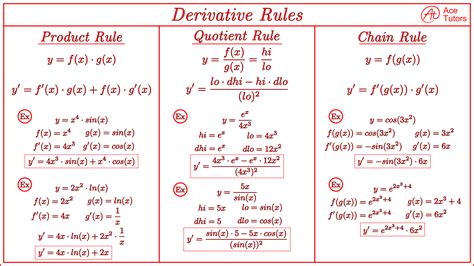
Method 4: Using Differentiation Rules

Differentiation rules provide a powerful way to find derivatives without using the limit form. There are several differentiation rules, including the power rule, product rule, quotient rule, and chain rule.
Consider the function f(x) = x^2. Using the power rule, we can find the derivative of f(x) as follows:
f'(x) = 2x
Example: Finding the Derivative Using Differentiation Rules
Find the derivative of the function f(x) = 3x^2 using the power rule.
Solution: Using the power rule, we can find the derivative of f(x) as follows:
f'(x) = 6x
Method 5: Using Graphical Analysis

Graphical analysis provides a visual way to understand derivatives in limit form. By analyzing the graph of a function, you can determine the rate of change of the function at a specific point.
Consider the function f(x) = x^2. The graph of f(x) shows that the rate of change of the function at x = 2 is 4.
Example: Finding the Derivative Using Graphical Analysis
Find the derivative of the function f(x) = 3x using graphical analysis.
Solution: The graph of f(x) shows that the rate of change of the function at x = 4 is 3.
What is the limit form of a derivative?
+The limit form of a derivative is a mathematical expression that represents the rate of change of a function at a specific point. It's defined as the limit of the average rate of change of the function as the change in the input approaches zero.
Why is it important to understand derivatives in limit form?
+Understanding derivatives in limit form is crucial in various fields, such as physics, engineering, and economics. It allows us to analyze complex problems, make informed decisions, and drive innovation.
How can I visualize the derivative as a slope?
+The derivative of a function at a point represents the slope of the tangent line to the graph of the function at that point. You can visualize the derivative as a slope by drawing a graph of the function and finding the slope of the tangent line at a specific point.
By mastering the five methods outlined in this article, you'll gain a deep understanding of derivatives in limit form and unlock the full potential of calculus. Remember to practice regularly and apply these concepts to real-world problems to reinforce your learning. Share your thoughts, ask questions, and explore the world of calculus with confidence!