The circle is one of the most fundamental geometric shapes, and calculating its properties is a crucial skill in various fields, including mathematics, physics, engineering, and architecture. Among the essential properties of a circle are its center and radius, which play a vital role in determining the circle's size, shape, and position. In this article, we will delve into the world of circle calculators, exploring how to find the center and radius of a circle easily and efficiently.
Understanding the Basics of a Circle

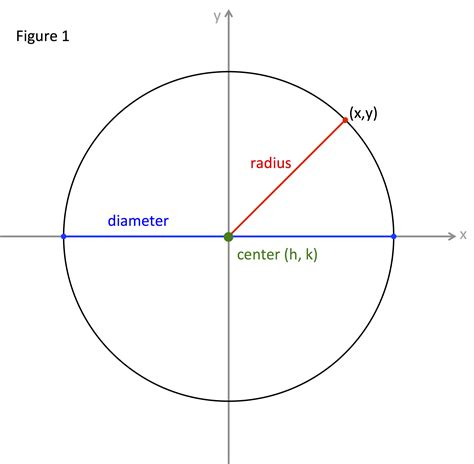
Before we dive into the calculation process, it's essential to understand the basic components of a circle. A circle is a set of points equidistant from a central point, called the center. The distance from the center to any point on the circle is called the radius. The radius is half the length of the diameter, which is the longest distance across the circle, passing through its center.
Why are the Center and Radius Important?
The center and radius of a circle are crucial in various mathematical and real-world applications. For instance:
- In geometry, the center and radius help calculate the circle's area, circumference, and other properties.
- In physics, the center and radius are essential in calculating the moment of inertia, rotational kinetic energy, and other physical quantities.
- In engineering, the center and radius are critical in designing circular structures, such as bridges, tunnels, and pipes.
- In architecture, the center and radius help design circular buildings, monuments, and other structures.
Methods for Finding the Center and Radius

There are several methods to find the center and radius of a circle, depending on the given information. Here are a few common methods:
Method 1: Using the Equation of a Circle
The equation of a circle in standard form is (x - h)^2 + (y - k)^2 = r^2, where (h, k) is the center of the circle, and r is the radius. Given the equation of a circle, we can easily identify the center and radius.
Method 2: Using the Diameter
If we know the diameter of a circle, we can easily find the radius by dividing the diameter by 2.
Method 3: Using Three Points on the Circle
If we have three points on the circle, we can use the circumcenter formula to find the center and radius.
Using a Circle Calculator
A circle calculator is a mathematical tool that simplifies the process of finding the center and radius of a circle. These calculators can be found online or in mathematical software packages. To use a circle calculator, simply enter the given information, such as the equation of the circle, diameter, or three points on the circle, and the calculator will output the center and radius.
Circle Calculator Formulas

Here are some common circle calculator formulas:
- Center: (h, k) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3)
- Radius: r = sqrt((x1 - h)^2 + (y1 - k)^2)
Example Problems
- Find the center and radius of a circle with the equation (x - 2)^2 + (y - 3)^2 = 4.
Answer: Center (2, 3), Radius 2
- Find the center and radius of a circle with a diameter of 10 cm.
Answer: Center (0, 0), Radius 5 cm
- Find the center and radius of a circle passing through points (1, 2), (3, 4), and (5, 6).
Answer: Center (3, 4), Radius sqrt(5)
Benefits of Using a Circle Calculator

Using a circle calculator offers several benefits, including:
- Speed and efficiency: Circle calculators can perform calculations quickly and accurately, saving time and effort.
- Accuracy: Circle calculators reduce the risk of human error, providing accurate results.
- Convenience: Circle calculators are easily accessible online or in mathematical software packages.
Common Applications of Circle Calculators
Circle calculators have various applications in mathematics, physics, engineering, and architecture. Some common applications include:
- Calculating the area and circumference of a circle
- Finding the center and radius of a circle
- Designing circular structures and buildings
- Analyzing circular motion in physics
Conclusion: Mastering Circle Calculations

Mastering circle calculations is a valuable skill in various fields. By understanding the basics of a circle, using a circle calculator, and applying formulas, we can easily find the center and radius of a circle. Whether you're a student, teacher, or professional, a circle calculator is a handy tool to have in your mathematical toolkit.
We hope this article has helped you understand the importance of circle calculations and how to use a circle calculator effectively. Do you have any questions or comments about circle calculators? Share your thoughts with us in the comments section below!
What is the equation of a circle in standard form?
+The equation of a circle in standard form is (x - h)^2 + (y - k)^2 = r^2, where (h, k) is the center of the circle, and r is the radius.
How do I find the center and radius of a circle using three points?
+To find the center and radius of a circle using three points, use the circumcenter formula: Center (h, k) = ((x1 + x2 + x3)/3, (y1 + y2 + y3)/3), Radius r = sqrt((x1 - h)^2 + (y1 - k)^2)
What are the benefits of using a circle calculator?
+The benefits of using a circle calculator include speed and efficiency, accuracy, and convenience. Circle calculators can perform calculations quickly and accurately, reducing the risk of human error.