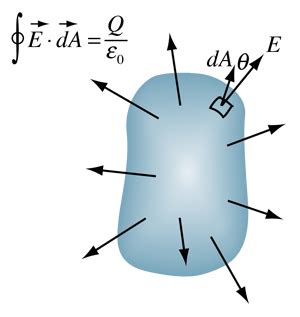
Gauss's Law is a fundamental concept in physics, particularly in the study of electromagnetism. It helps us understand the behavior of electric charges and the resulting electric fields. The law is named after Carl Friedrich Gauss, a German mathematician and physicist who first formulated it in the 19th century. In this article, we'll delve into the integral form of Gauss's Law, exploring its significance, mathematical representation, and practical applications.
Gauss's Law is a powerful tool for calculating the electric flux through a closed surface, which is essential in understanding various phenomena in physics and engineering. The law has far-reaching implications in fields such as electrical engineering, materials science, and optics. By grasping the integral form of Gauss's Law, you'll gain a deeper understanding of the intricate relationships between electric charges, electric fields, and the resulting flux.
What is Gauss's Law?

Gauss's Law states that the total electric flux through a closed surface is proportional to the charge enclosed within that surface. Mathematically, this is represented as:
∮E⋅dA = Q/ε₀
where:
- ∮E⋅dA is the electric flux through the closed surface
- Q is the total charge enclosed within the surface
- ε₀ is the electric constant (also known as the permittivity of free space)
The left-hand side of the equation represents the electric flux, which is the dot product of the electric field (E) and the area vector (dA) integrated over the entire closed surface. The right-hand side represents the total charge enclosed within the surface, divided by the electric constant.
Understanding the Integral Form
The integral form of Gauss's Law is a mathematical representation of the law, which allows us to calculate the electric flux through a closed surface. The integral form is written as:
∮E⋅dA = ∫∫(∇⋅E)dV
where:
- ∮E⋅dA is the electric flux through the closed surface
- ∫∫(∇⋅E)dV is the volume integral of the divergence of the electric field
The divergence of the electric field (∇⋅E) represents the amount of electric flux emanating from a given point in space. By integrating this divergence over the entire volume enclosed by the surface, we obtain the total electric flux through the surface.
Key Concepts and Applications

Gauss's Law has numerous applications in physics and engineering, including:
- Electric field calculations: Gauss's Law allows us to calculate the electric field at a given point in space, given the distribution of charges and the geometry of the surrounding surface.
- Electrostatic shielding: Gauss's Law helps us understand how to design electrostatic shields, which are used to protect sensitive electronic equipment from external electromagnetic interference.
- Capacitor design: Gauss's Law is essential in the design of capacitors, which store electrical energy. By optimizing the geometry of the capacitor plates and the dielectric material, engineers can increase the capacitance and reduce the size of the capacitor.
Practical Examples and Problem-Solving
To illustrate the application of Gauss's Law, let's consider a simple example:
Problem: A point charge of +2 μC is placed at the center of a spherical surface with a radius of 0.5 m. Calculate the electric flux through the surface.
Solution: Using Gauss's Law, we can calculate the electric flux as:
∮E⋅dA = Q/ε₀ = (2 μC)/(8.85 × 10^(-12) F/m) = 225.7 Nm^2/C
This result represents the total electric flux through the spherical surface.
Conclusion and Future Directions

In this article, we've explored the integral form of Gauss's Law, its significance, and practical applications. By mastering this fundamental concept, you'll gain a deeper understanding of the intricate relationships between electric charges, electric fields, and the resulting flux. As technology continues to advance, the importance of Gauss's Law will only grow, with applications in emerging fields such as nanotechnology, biophysics, and renewable energy.
We hope this article has inspired you to delve deeper into the world of electromagnetism and explore the many wonders that await discovery. Share your thoughts and questions in the comments section below, and let's continue the conversation!
What is the difference between Gauss's Law and Coulomb's Law?
+Gauss's Law and Coulomb's Law are both fundamental laws in electromagnetism, but they describe different aspects of electric charges and fields. Gauss's Law relates the electric flux through a closed surface to the charge enclosed within that surface, while Coulomb's Law describes the force between two point charges.
How does Gauss's Law apply to real-world problems?
+Gauss's Law has numerous practical applications in fields such as electrical engineering, materials science, and optics. It helps us design electrostatic shields, capacitors, and other electronic devices, and is essential in understanding various phenomena in physics and engineering.
Can Gauss's Law be applied to non-uniform charge distributions?
+Yes, Gauss's Law can be applied to non-uniform charge distributions. However, the calculation of the electric flux may become more complex, requiring the use of more advanced mathematical techniques and numerical methods.