Form A Polynomial With Given Real Zeros And Degree

Quick Links :

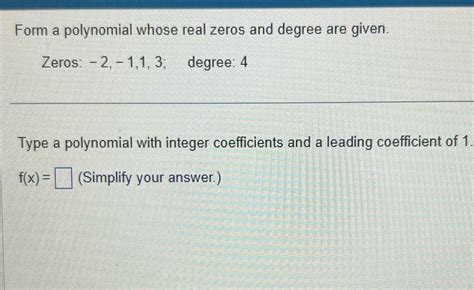
Polynomials are a fundamental concept in mathematics, and understanding how to form them with given real zeros and a degree is essential for problem-solving in algebra and other branches of mathematics. In this article, we will delve into the world of polynomials, exploring what they are, their importance, and a step-by-step guide on how to form a polynomial with given real zeros and a degree.

What are Polynomials?

Polynomials are algebraic expressions consisting of variables and coefficients combined using only addition, subtraction, and multiplication, and with non-negative integer exponents. For instance, x^2 + 3x - 4 is a polynomial because it follows these rules. Polynomials can have one or more terms, and they play a crucial role in various mathematical and real-world applications, including solving equations, modeling real-world phenomena, and making predictions.

Importance of Polynomials

The importance of polynomials cannot be overstated. They are used extensively in various fields, including physics, engineering, computer science, and economics. Polynomials help in modeling complex systems, solving equations, and making predictions. They are also used in data analysis, machine learning, and cryptography. Understanding polynomials and their properties is essential for problem-solving in these fields.

What are Real Zeros of a Polynomial?

The real zeros of a polynomial are the values of x that make the polynomial equal to zero. In other words, they are the roots of the polynomial equation. For instance, if we have a polynomial x^2 + 3x - 4, the real zeros are the values of x that satisfy the equation x^2 + 3x - 4 = 0. Real zeros can be positive, negative, or zero.

How to Form a Polynomial with Given Real Zeros and Degree

Forming a polynomial with given real zeros and a degree involves several steps. Here's a step-by-step guide:

Step 1: Identify the Real Zeros

The first step is to identify the real zeros of the polynomial. Let's say we have two real zeros, x = a and x = b.

Step 2: Determine the Degree

Next, we need to determine the degree of the polynomial. The degree of a polynomial is the highest power of the variable. For instance, if we have a polynomial x^3 + 2x^2 - 3x - 4, the degree is 3.

Step 3: Write the Factors

Using the real zeros, we can write the factors of the polynomial. For instance, if we have real zeros x = a and x = b, the factors will be (x - a) and (x - b).

Step 4: Multiply the Factors

To form the polynomial, we need to multiply the factors. For instance, if we have factors (x - a) and (x - b), the polynomial will be (x - a)(x - b).

Step 5: Add a Leading Coefficient (Optional)

If we want to add a leading coefficient to the polynomial, we can do so. The leading coefficient is the coefficient of the highest power of the variable.

Example

Let's say we want to form a polynomial with real zeros x = 2 and x = -3 and a degree of 2. Here's how we can do it:

• Identify the real zeros: x = 2 and x = -3
• Determine the degree: 2
• Write the factors: (x - 2) and (x + 3)
• Multiply the factors: (x - 2)(x + 3) = x^2 + x - 6

Forming a Polynomial with More Than Two Real Zeros

If we have more than two real zeros, we can form a polynomial by multiplying the factors. For instance, if we have real zeros x = a, x = b, and x = c, the polynomial will be (x - a)(x - b)(x - c).

Forming a Polynomial with a Given Degree and No Real Zeros

If we have a given degree and no real zeros, we can form a polynomial by using the degree and a leading coefficient. For instance, if we have a degree of 3 and a leading coefficient of 2, the polynomial will be 2x^3.

Common Applications of Polynomials

Polynomials have numerous applications in various fields, including physics, engineering, computer science, and economics. Some common applications include:

• Modeling complex systems
• Solving equations
• Making predictions
• Data analysis
• Machine learning
• Cryptography

Conclusion

Forming a polynomial with given real zeros and a degree is a fundamental concept in mathematics. By following the steps outlined in this article, you can easily form a polynomial with given real zeros and a degree. Remember to identify the real zeros, determine the degree, write the factors, multiply the factors, and add a leading coefficient (optional). Polynomials have numerous applications in various fields, and understanding how to form them is essential for problem-solving and critical thinking.

We hope you found this article informative and helpful. If you have any questions or comments, please feel free to share them with us. Don't forget to share this article with your friends and colleagues who may find it useful.