Expanded Form In Exponents: Simplified Explanation

Quick Links :

The world of exponents can be intimidating, but with a solid understanding of expanded form, you'll be well on your way to mastering this fundamental math concept. In this article, we'll delve into the concept of expanded form in exponents, providing a simplified explanation that's easy to grasp.

Exponents are a shorthand way of expressing repeated multiplication, making them an essential tool in mathematics. The expanded form of an exponent is a way of expressing this repeated multiplication in a more detailed manner. By understanding the expanded form, you'll gain a deeper appreciation for how exponents work and be able to tackle more complex math problems with confidence.

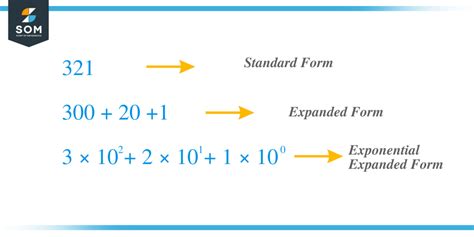
What is Expanded Form in Exponents?

Expanded form in exponents refers to the process of expressing an exponent as a series of repeated multiplications. For example, consider the expression 2^3. In expanded form, this would be written as:

2 × 2 × 2

This expanded form shows that 2^3 is equal to 2 multiplied by itself three times.

Benefits of Expanded Form

So, why is it important to understand the expanded form of exponents? Here are a few key benefits:

• Improved understanding: By breaking down exponents into their expanded form, you'll gain a deeper understanding of how they work.
• Simplified calculations: Expanded form can make it easier to perform calculations involving exponents, especially when dealing with more complex expressions.
• Better problem-solving skills: Mastering the expanded form of exponents will help you tackle more challenging math problems with confidence.

How to Write Exponents in Expanded Form

Writing exponents in expanded form is a straightforward process. Here are the steps:

1. Identify the base: The base is the number being raised to the power. In the example 2^3, the base is 2.
2. Identify the exponent: The exponent is the power to which the base is being raised. In this case, the exponent is 3.
3. Write the expanded form: Multiply the base by itself as many times as indicated by the exponent. For 2^3, this would be:

2 × 2 × 2

Examples of Expanded Form in Exponents

Here are a few more examples of writing exponents in expanded form:

• 3^2 = 3 × 3
• 4^1 = 4 (since any number raised to the power of 1 is equal to itself)
• 5^4 = 5 × 5 × 5 × 5

Common Mistakes to Avoid

When working with exponents, it's easy to make mistakes. Here are a few common pitfalls to avoid:

• Forgetting the base: Make sure to identify the base correctly, as this can greatly affect the expanded form.
• Miscounting the exponent: Double-check the exponent to ensure you're multiplying the base the correct number of times.
• Mixing up the order of operations: When working with multiple exponents, make sure to follow the correct order of operations (PEMDAS/BODMAS).

Real-World Applications of Expanded Form

Understanding the expanded form of exponents has numerous real-world applications, including:

• Science and engineering: Exponents are used to describe the laws of physics and engineering, making them crucial for scientists and engineers.
• Computer programming: Exponents are used in programming languages to perform calculations and manipulate data.
• Finance and economics: Exponents are used in finance to calculate interest rates, investment returns, and other economic indicators.

Conclusion and Next Steps

In conclusion, understanding the expanded form of exponents is a fundamental concept in mathematics. By mastering this concept, you'll gain a deeper understanding of how exponents work and be able to tackle more complex math problems with confidence. Remember to practice writing exponents in expanded form and avoid common mistakes to ensure you're working with exponents accurately.

We hope this article has helped you grasp the concept of expanded form in exponents. Do you have any questions or topics you'd like to discuss? Share your thoughts in the comments below!