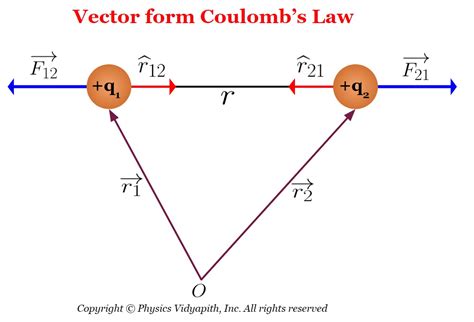
The fundamental principles of physics are the building blocks of our understanding of the natural world. One such principle is Coulomb's Law, which describes the interaction between electric charges. In this article, we will delve into the vector form of Coulomb's Law, exploring its intricacies and providing examples to solidify your understanding.

Coulomb's Law is a crucial concept in electromagnetism, describing the force between two point charges. The law states that the force between two charges is proportional to the product of the charges and inversely proportional to the square of the distance between them. While the scalar form of Coulomb's Law is widely known, the vector form provides a more comprehensive understanding of the interaction.
Vector Form of Coulomb's Law
The vector form of Coulomb's Law is a mathematical representation of the force between two charges, taking into account the direction of the force. This form is essential in understanding the behavior of electric charges in various situations.

Mathematically, the vector form of Coulomb's Law can be expressed as:
F = k * (q1 * q2) / r^2 * r̂
where:
- F is the force between the charges
- k is Coulomb's constant (approximately 8.99 x 10^9 N m^2 C^-2)
- q1 and q2 are the magnitudes of the charges
- r is the distance between the charges
- r̂ is the unit vector in the direction of the force
Understanding the Unit Vector
The unit vector r̂ plays a crucial role in the vector form of Coulomb's Law. It represents the direction of the force between the charges. To calculate the unit vector, we need to know the position vectors of the charges.

For example, consider two charges q1 and q2 located at positions r1 and r2, respectively. The position vector r can be calculated as:
r = r2 - r1
The unit vector r̂ can then be calculated as:
r̂ = r / |r|
where |r| is the magnitude of the position vector.
Examples and Applications
To illustrate the application of the vector form of Coulomb's Law, let's consider a few examples:
Example 1: Two Charges on the x-axis
Suppose we have two charges q1 = 2 μC and q2 = -3 μC located on the x-axis at x1 = 2 m and x2 = 5 m, respectively.

To calculate the force between the charges, we need to find the position vector r and the unit vector r̂.
r = x2 - x1 = 5 m - 2 m = 3 m
r̂ = r / |r| = (3 m) / |3 m| = 1
The force between the charges can now be calculated using the vector form of Coulomb's Law:
F = k * (q1 * q2) / r^2 * r̂ = (8.99 x 10^9 N m^2 C^-2) * (2 μC * -3 μC) / (3 m)^2 * 1 = -6.67 x 10^-5 N
Example 2: Three Charges in a Triangle
Consider three charges q1 = 4 μC, q2 = -2 μC, and q3 = 1 μC located at the vertices of a triangle with sides of length 3 m, 4 m, and 5 m.

To calculate the force between each pair of charges, we need to find the position vectors and unit vectors for each pair.
The vector form of Coulomb's Law can be applied to each pair of charges to calculate the forces.
Conclusion and Future Directions
In conclusion, the vector form of Coulomb's Law provides a powerful tool for understanding the interaction between electric charges. By considering the direction of the force, we can gain a deeper understanding of the behavior of charges in various situations.
As you continue to explore the world of electromagnetism, remember to apply the vector form of Coulomb's Law to complex problems involving multiple charges. With practice and patience, you'll become proficient in using this fundamental principle to analyze and solve a wide range of problems.
We encourage you to share your thoughts and questions in the comments section below. How do you think the vector form of Coulomb's Law can be applied to real-world problems? Share your ideas and let's continue the conversation!
What is the main difference between the scalar and vector forms of Coulomb's Law?
+The scalar form of Coulomb's Law only provides the magnitude of the force between charges, while the vector form provides both the magnitude and direction of the force.
How do I calculate the unit vector in the vector form of Coulomb's Law?
+To calculate the unit vector, you need to know the position vectors of the charges. The unit vector can be calculated as r̂ = r / |r|, where r is the position vector and |r| is its magnitude.
Can I use the vector form of Coulomb's Law to calculate the force between multiple charges?
+Yes, the vector form of Coulomb's Law can be applied to each pair of charges to calculate the forces. You'll need to calculate the position vectors and unit vectors for each pair of charges.