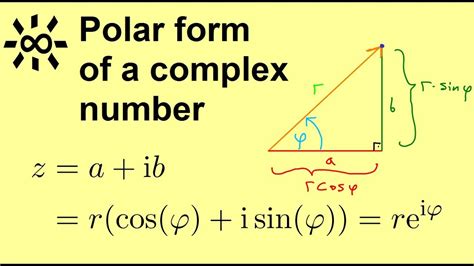Convert To Polar Form: Simplify Complex Numbers

Quick Links :

The world of complex numbers! It's a fascinating realm where numbers have both magnitude and direction. In this article, we'll delve into the process of converting complex numbers to polar form, which is a fundamental concept in mathematics, physics, and engineering.

Why Convert to Polar Form?

Converting complex numbers to polar form is essential for various reasons. Firstly, it provides a more intuitive understanding of complex numbers, making it easier to visualize and work with them. Secondly, polar form is crucial for solving equations involving complex numbers, as it allows us to use trigonometric identities and formulas. Lastly, polar form is a prerequisite for advanced mathematical concepts, such as complex analysis and signal processing.

What is Polar Form?

Polar form represents a complex number as a magnitude (length) and an angle (direction). It's denoted as:

z = r(cosθ + isinθ)

where:

• z is the complex number
• r is the magnitude (length)
• θ is the angle (direction)
• i is the imaginary unit (i = √(-1))

How to Convert to Polar Form

Converting a complex number to polar form involves finding its magnitude and angle. Here's a step-by-step guide:

1. Find the magnitude (r): The magnitude is the distance from the origin to the point representing the complex number in the complex plane. It's calculated using the Pythagorean theorem:

r = √(a^2 + b^2)

where a and b are the real and imaginary parts of the complex number, respectively.

2. Find the angle (θ): The angle is measured counterclockwise from the positive real axis. It can be found using the following formulas:

θ = arctan(b/a)

or

θ = arctan2(b, a)

The arctan2 function is used to handle the case where a = 0, which would result in an undefined value for arctan.

Example: Convert 3 + 4i to Polar Form

Let's apply the conversion process to the complex number 3 + 4i.

1. Find the magnitude:

r = √(3^2 + 4^2) = √(9 + 16) = √25 = 5

2. Find the angle:

θ = arctan(4/3) ≈ 53.13°

So, the polar form of 3 + 4i is:

z = 5(cos(53.13°) + isin(53.13°))

Benefits of Polar Form

Converting complex numbers to polar form offers several benefits:

• Simplifies complex calculations: Polar form makes it easier to perform operations like multiplication, division, and exponentiation.
• Provides a geometric interpretation: Polar form allows us to visualize complex numbers as vectors in the complex plane.
• Facilitates trigonometric identities: Polar form enables us to use trigonometric identities and formulas, making it easier to solve equations.

Common Applications of Polar Form

Polar form is used in various fields, including:

• Electrical engineering: Polar form is essential for analyzing AC circuits and impedance.
• Signal processing: Polar form is used in signal processing techniques like filtering and modulation.
• Navigation: Polar form is used in navigation systems, such as GPS, to calculate distances and angles.

Challenges and Limitations

While polar form offers many advantages, it also presents some challenges and limitations:

• Ambiguity in angle: The angle θ can have multiple values, which can lead to ambiguity in certain calculations.
• Difficulty in representing complex numbers with negative magnitudes: Polar form can become complicated when dealing with complex numbers having negative magnitudes.

Best Practices for Working with Polar Form

To overcome the challenges and limitations of polar form, follow these best practices:

• Use the arctan2 function: When finding the angle, use the arctan2 function to handle the case where a = 0.
• Be aware of ambiguity in angle: When working with polar form, be mindful of the possibility of multiple angles.

Conclusion: Unlocking the Power of Polar Form

Converting complex numbers to polar form is a fundamental skill that can unlock the power of complex analysis and signal processing. By understanding the process and benefits of polar form, you'll be better equipped to tackle complex problems in mathematics, physics, and engineering.

Now it's your turn! Share your thoughts and experiences with polar form in the comments below. How do you use polar form in your work or studies? What challenges have you faced, and how have you overcome them?