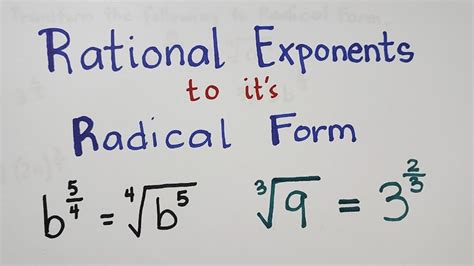Radicals and exponential forms are two fundamental concepts in mathematics, particularly in algebra and calculus. While radicals are used to represent the roots of numbers, exponential forms represent repeated multiplication. Converting radicals to exponential form can be a challenging task, but it's a crucial skill to master for solving complex mathematical problems. In this article, we will explore five ways to convert radicals to exponential form, along with practical examples and explanations.
Understanding Radicals and Exponential Forms

Before we dive into the conversion methods, let's quickly review the basics of radicals and exponential forms. A radical is a mathematical expression that represents the root of a number. For example, √16 represents the square root of 16. On the other hand, exponential forms represent repeated multiplication. For instance, 2^3 represents 2 multiplied by itself three times.
Radical Notation vs. Exponential Notation
Radical notation and exponential notation are two different ways to represent the same mathematical concept. Radical notation uses a radical symbol (√) to represent the root of a number, while exponential notation uses a base and an exponent to represent repeated multiplication.
Method 1: Using the Definition of Exponents

One way to convert radicals to exponential form is by using the definition of exponents. According to this definition, a^m × a^n = a^(m+n). We can use this property to rewrite a radical expression in exponential form.
For example, let's convert √16 to exponential form. We can rewrite 16 as 2^4, since 2 multiplied by itself four times equals 16. Using the definition of exponents, we can rewrite √16 as (2^4)^(1/2) = 2^(4/2) = 2^2.
Example 1: Converting √16 to Exponential Form
| Radical Form | Exponential Form |
|---|---|
| √16 | 2^2 |
Method 2: Using the Properties of Exponents

Another way to convert radicals to exponential form is by using the properties of exponents. One useful property is that a^(m/n) = (a^m)^(1/n). We can use this property to rewrite a radical expression in exponential form.
For example, let's convert ³√27 to exponential form. We can rewrite 27 as 3^3, since 3 multiplied by itself three times equals 27. Using the property of exponents, we can rewrite ³√27 as (3^3)^(1/3) = 3^(3/3) = 3^1.
Example 2: Converting ³√27 to Exponential Form
| Radical Form | Exponential Form |
|---|---|
| ³√27 | 3^1 |
Method 3: Using the Power Rule of Exponents

The power rule of exponents states that (a^m)^n = a^(m*n). We can use this rule to rewrite a radical expression in exponential form.
For example, let's convert √(2^6) to exponential form. Using the power rule of exponents, we can rewrite √(2^6) as (2^6)^(1/2) = 2^(6/2) = 2^3.
Example 3: Converting √(2^6) to Exponential Form
| Radical Form | Exponential Form |
|---|---|
| √(2^6) | 2^3 |
Method 4: Using the Product Rule of Exponents

The product rule of exponents states that a^m × a^n = a^(m+n). We can use this rule to rewrite a radical expression in exponential form.
For example, let's convert √(2^3 × 2^2) to exponential form. Using the product rule of exponents, we can rewrite √(2^3 × 2^2) as √(2^(3+2)) = √(2^5) = (2^5)^(1/2) = 2^(5/2).
Example 4: Converting √(2^3 × 2^2) to Exponential Form
| Radical Form | Exponential Form |
|---|---|
| √(2^3 × 2^2) | 2^(5/2) |
Method 5: Using the Quotient Rule of Exponents

The quotient rule of exponents states that a^m ÷ a^n = a^(m-n). We can use this rule to rewrite a radical expression in exponential form.
For example, let's convert √(2^6 ÷ 2^2) to exponential form. Using the quotient rule of exponents, we can rewrite √(2^6 ÷ 2^2) as √(2^(6-2)) = √(2^4) = (2^4)^(1/2) = 2^(4/2) = 2^2.
Example 5: Converting √(2^6 ÷ 2^2) to Exponential Form
| Radical Form | Exponential Form |
|---|---|
| √(2^6 ÷ 2^2) | 2^2 |
By mastering these five methods, you'll be able to convert radicals to exponential form with ease. Remember to practice regularly and apply these methods to different types of problems.
We hope this article has helped you understand the concept of converting radicals to exponential form. If you have any questions or need further clarification, please don't hesitate to ask.
What is the main difference between radical notation and exponential notation?
+Raised notation uses a raised symbol (^) to represent repeated multiplication, while exponential notation uses a base and an exponent to represent repeated multiplication.
Can you convert any radical expression to exponential form?
+Not all radical expressions can be converted to exponential form. However, many radical expressions can be rewritten in exponential form using the methods outlined in this article.
What is the power rule of exponents?
+The power rule of exponents states that (a^m)^n = a^(m*n).