Square Root Of 15 In Radical Form Simplified

Quick Links :

The concept of square roots is a fundamental aspect of mathematics, particularly in algebra and geometry. It is essential to understand the concept of square roots, as it plays a crucial role in solving various mathematical problems. In this article, we will delve into the world of square roots, focusing specifically on the square root of 15 in radical form simplified.

What is a Square Root?

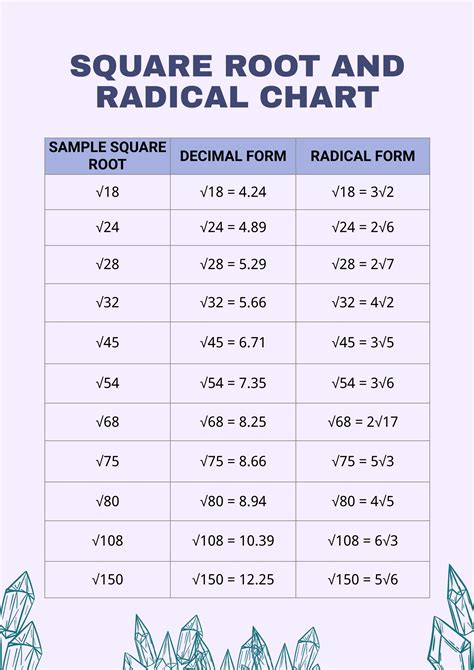
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because 4 multiplied by 4 equals 16. Square roots can be expressed in two forms: decimal form and radical form. The decimal form represents the square root as a numerical value, while the radical form represents it using the radical symbol (√).

What is Radical Form?

Radical form is a way of expressing square roots using the radical symbol (√). This symbol is used to indicate that the number inside the radical is being taken as a square root. For instance, the square root of 16 in radical form is written as √16. Radical form is often used to simplify complex mathematical expressions and to make calculations easier.

Simplifying Square Roots in Radical Form

When simplifying square roots in radical form, the goal is to find the simplest radical form of the expression. This involves factoring out perfect squares from under the radical sign. For example, √12 can be simplified to √(4 × 3), which is equal to 2√3.

Calculating the Square Root of 15 in Radical Form

To calculate the square root of 15 in radical form, we need to factor out perfect squares from under the radical sign. We can start by finding the prime factorization of 15, which is 3 × 5. Since there are no perfect squares in the factorization, the square root of 15 in radical form is simply √15.

Steps to Simplify the Square Root of 15

Here are the steps to simplify the square root of 15 in radical form:

1. Find the prime factorization of 15, which is 3 × 5.
2. Look for perfect squares in the factorization. In this case, there are no perfect squares.
3. Write the square root of 15 in radical form as √15.

Practical Applications of Square Roots

Square roots have numerous practical applications in various fields, including:

• Geometry: Square roots are used to calculate distances and lengths in geometric shapes.
• Algebra: Square roots are used to solve quadratic equations and to simplify algebraic expressions.
• Physics: Square roots are used to calculate velocities and distances in physics problems.
• Engineering: Square roots are used to calculate stresses and loads in engineering problems.

Conclusion

In conclusion, the square root of 15 in radical form simplified is √15. Simplifying square roots in radical form involves factoring out perfect squares from under the radical sign. Understanding square roots and their applications is essential for solving various mathematical problems and for making calculations easier.