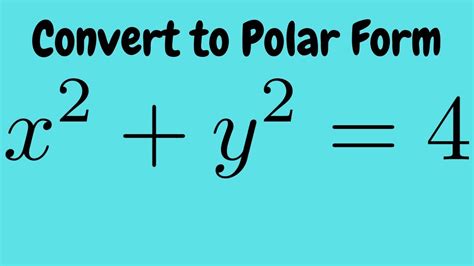Converting equations to polar form is a fundamental concept in mathematics, particularly in algebra and trigonometry. It's a crucial skill to master, as it enables us to represent complex numbers and equations in a more convenient and intuitive way. In this article, we'll delve into the world of polar form equations, exploring the benefits, working mechanisms, and practical examples.
Understanding Polar Form

Polar form is a way of expressing complex numbers and equations using the distance from the origin (r) and the angle formed with the positive x-axis (θ). This representation is particularly useful when dealing with equations involving trigonometric functions, as it allows us to visualize and analyze the relationships between variables more easily.
Benefits of Polar Form
The polar form has several advantages over other forms of representation:
- Simplifies complex equations: Polar form can simplify complex equations involving trigonometric functions, making them easier to solve and analyze.
- Facilitates visualization: The polar form provides a clear and intuitive way to visualize complex numbers and equations, making it easier to understand their behavior and relationships.
- Streamlines calculations: Polar form can reduce the number of calculations required to solve equations, making it a more efficient and effective method.
Converting Equations to Polar Form

Converting equations to polar form involves expressing the equation in terms of the distance from the origin (r) and the angle formed with the positive x-axis (θ). Here's a step-by-step guide to converting equations to polar form:
- Identify the equation: Start by identifying the equation you want to convert to polar form.
- Determine the distance from the origin: Calculate the distance from the origin (r) using the equation r = √(x^2 + y^2).
- Determine the angle: Calculate the angle formed with the positive x-axis (θ) using the equation θ = arctan(y/x).
- Express the equation in polar form: Rewrite the equation in terms of r and θ.
Practical Examples
Let's consider a few practical examples to illustrate the conversion process:
- Example 1: Convert the equation x^2 + y^2 = 4 to polar form.
- Determine the distance from the origin: r = √(x^2 + y^2) = 2.
- Determine the angle: θ = arctan(y/x).
- Express the equation in polar form: r^2 = 4.
- Example 2: Convert the equation x^2 - y^2 = 3 to polar form.
- Determine the distance from the origin: r = √(x^2 + y^2).
- Determine the angle: θ = arctan(y/x).
- Express the equation in polar form: r^2cos(2θ) = 3.
Working Mechanisms of Polar Form

The polar form works by using the distance from the origin (r) and the angle formed with the positive x-axis (θ) to represent complex numbers and equations. This representation enables us to:
- Simplify complex equations: By expressing equations in terms of r and θ, we can simplify complex equations and make them easier to solve.
- Facilitate visualization: The polar form provides a clear and intuitive way to visualize complex numbers and equations, making it easier to understand their behavior and relationships.
- Streamline calculations: Polar form can reduce the number of calculations required to solve equations, making it a more efficient and effective method.
Steps to Convert Equations to Polar Form
Here are the steps to convert equations to polar form:
- Identify the equation: Start by identifying the equation you want to convert to polar form.
- Determine the distance from the origin: Calculate the distance from the origin (r) using the equation r = √(x^2 + y^2).
- Determine the angle: Calculate the angle formed with the positive x-axis (θ) using the equation θ = arctan(y/x).
- Express the equation in polar form: Rewrite the equation in terms of r and θ.
Common Applications of Polar Form

Polar form has numerous applications in various fields, including:
- Electrical engineering: Polar form is used to represent and analyze complex electrical circuits.
- Signal processing: Polar form is used to represent and analyze signals in signal processing.
- Navigation: Polar form is used in navigation systems to represent and analyze complex navigation data.
Real-World Examples
Here are some real-world examples of the applications of polar form:
- Example 1: In electrical engineering, polar form is used to represent and analyze complex electrical circuits.
- Example 2: In signal processing, polar form is used to represent and analyze signals.
- Example 3: In navigation, polar form is used to represent and analyze complex navigation data.
What is polar form?
+Polar form is a way of expressing complex numbers and equations using the distance from the origin (r) and the angle formed with the positive x-axis (θ).
How do I convert an equation to polar form?
+To convert an equation to polar form, identify the equation, determine the distance from the origin (r), determine the angle (θ), and express the equation in terms of r and θ.
What are the benefits of polar form?
+The benefits of polar form include simplifying complex equations, facilitating visualization, and streamlining calculations.
In conclusion, converting equations to polar form is a powerful tool for simplifying complex equations, facilitating visualization, and streamlining calculations. By understanding the benefits, working mechanisms, and practical examples of polar form, you can unlock the full potential of this powerful mathematical concept. So, go ahead and start exploring the world of polar form equations today!