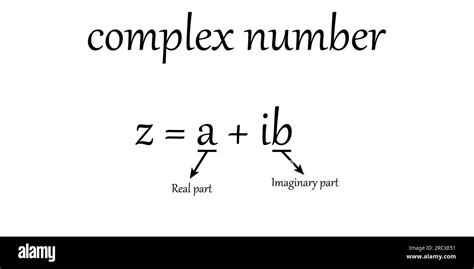Understanding Complex Numbers and Their Importance in Mathematics

Complex numbers are a fundamental concept in mathematics, extending the real number system to include imaginary numbers. They have numerous applications in various fields, such as engineering, physics, and computer science. In this article, we will explore the concept of complex numbers, their importance, and how to convert them to standard form using a calculator tool.
What are Complex Numbers?
Complex numbers are numbers that have both real and imaginary parts. They are denoted by the symbol "i" and can be expressed in the form a + bi, where a is the real part and bi is the imaginary part. The real part represents the x-coordinate, while the imaginary part represents the y-coordinate on the complex plane.
Key Concepts in Complex Numbers
Before diving deeper into complex numbers, it's essential to understand the key concepts:
- Imaginary unit (i): The imaginary unit is defined as the square root of -1, denoted by the symbol "i".
- Real part: The real part of a complex number is the part that is not multiplied by i.
- Imaginary part: The imaginary part of a complex number is the part that is multiplied by i.
- Complex conjugate: The complex conjugate of a complex number is obtained by changing the sign of the imaginary part.
Why are Complex Numbers Important?
Complex numbers have numerous applications in various fields, including:
- Electrical engineering: Complex numbers are used to analyze and design electrical circuits, particularly in the context of AC circuits.
- Signal processing: Complex numbers are used to represent and analyze signals in the frequency domain.
- Control theory: Complex numbers are used to analyze and design control systems.
- Quantum mechanics: Complex numbers are used to describe the behavior of particles in quantum mechanics.
Converting Complex Numbers to Standard Form

The standard form of a complex number is a + bi, where a is the real part and bi is the imaginary part. To convert a complex number to standard form, we can use the following steps:
- Simplify the expression: Simplify the given complex number expression by combining like terms.
- Write the expression in the form a + bi: Write the simplified expression in the form a + bi, where a is the real part and bi is the imaginary part.
Using a Complex Numbers to Standard Form Calculator Tool
A complex numbers to standard form calculator tool can simplify the process of converting complex numbers to standard form. These tools are available online and can be used to:
- Enter the complex number expression: Enter the complex number expression into the calculator tool.
- Simplify the expression: The calculator tool will simplify the expression and write it in standard form.
- View the result: View the result in standard form, a + bi.
Benefits of Using a Complex Numbers to Standard Form Calculator Tool
Using a complex numbers to standard form calculator tool has several benefits, including:
- Saves time: Using a calculator tool can save time and effort in converting complex numbers to standard form.
- Improves accuracy: Calculator tools can improve accuracy by reducing the risk of human error.
- Enhances understanding: Using a calculator tool can help students and professionals understand the concept of complex numbers and standard form.
Practical Examples of Using a Complex Numbers to Standard Form Calculator Tool
Here are some practical examples of using a complex numbers to standard form calculator tool:
- Example 1: Convert the complex number 2 + 3i to standard form using a calculator tool.
- Example 2: Convert the complex number (1 + 2i) / (2 - 3i) to standard form using a calculator tool.
Conclusion and Next Steps
In conclusion, complex numbers are a fundamental concept in mathematics with numerous applications in various fields. Converting complex numbers to standard form is an essential skill that can be simplified using a calculator tool. We encourage readers to try out a complex numbers to standard form calculator tool and explore its benefits.
What is the importance of complex numbers in mathematics?
+Complex numbers are important in mathematics because they extend the real number system to include imaginary numbers, which have numerous applications in various fields, such as engineering, physics, and computer science.
How can I convert a complex number to standard form?
+To convert a complex number to standard form, simplify the expression and write it in the form a + bi, where a is the real part and bi is the imaginary part. You can use a complex numbers to standard form calculator tool to simplify the process.
What are the benefits of using a complex numbers to standard form calculator tool?
+Using a complex numbers to standard form calculator tool can save time, improve accuracy, and enhance understanding of the concept of complex numbers and standard form.