Axis Of Symmetry In Standard Form Explained Simply

Quick Links :

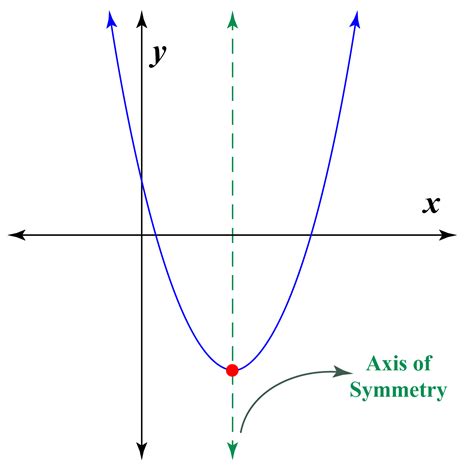
Understanding the concept of axis of symmetry in standard form is crucial in mathematics, particularly in geometry and algebra. The axis of symmetry is a fundamental concept that helps in understanding the properties of various geometric shapes and functions.

Mathematics is all around us, and understanding its concepts can make a significant difference in how we perceive and interact with the world. From the intricate patterns on a butterfly's wings to the majestic architecture of a skyscraper, mathematics plays a vital role in shaping our world. In this article, we will delve into the concept of axis of symmetry in standard form, exploring its definition, significance, and applications.

What is Axis of Symmetry in Standard Form?

The axis of symmetry is an imaginary line that divides a shape or a function into two equal halves, which are mirror images of each other. In the context of standard form, the axis of symmetry is typically represented by a vertical line, which is denoted by the equation x = a, where 'a' is a constant.

For example, consider a quadratic function in standard form, f(x) = ax^2 + bx + c. The axis of symmetry for this function is given by the equation x = -b/2a. This means that the graph of the function will be symmetrical about the vertical line x = -b/2a.

Significance of Axis of Symmetry

The axis of symmetry is a critical concept in mathematics, as it helps in understanding the properties of various geometric shapes and functions. Here are a few reasons why the axis of symmetry is significant:

• Symmetry: The axis of symmetry helps in identifying the symmetry of a shape or a function. By drawing the axis of symmetry, we can visualize the symmetry of the shape or function.
• Reflection: The axis of symmetry can be used to reflect a shape or a function across the axis. This is particularly useful in geometry, where we need to reflect shapes to create symmetrical patterns.
• Graphing: In algebra, the axis of symmetry is used to graph functions. By identifying the axis of symmetry, we can graph the function more accurately.

Types of Axis of Symmetry

There are several types of axis of symmetry, including:

• Vertical Axis of Symmetry: This is the most common type of axis of symmetry, which is represented by a vertical line. It is denoted by the equation x = a, where 'a' is a constant.
• Horizontal Axis of Symmetry: This type of axis of symmetry is represented by a horizontal line. It is denoted by the equation y = a, where 'a' is a constant.
• Oblique Axis of Symmetry: This type of axis of symmetry is represented by a slanted line. It is denoted by the equation y = mx + c, where 'm' is the slope and 'c' is the y-intercept.

How to Find the Axis of Symmetry

Finding the axis of symmetry is a straightforward process. Here are the steps to follow:

1. Identify the type of function: Determine the type of function, whether it is a quadratic function, a linear function, or a higher-degree polynomial function.
2. Write the equation in standard form: Write the equation in standard form, which is typically denoted by f(x) = ax^2 + bx + c.
3. Identify the coefficients: Identify the coefficients 'a', 'b', and 'c' in the equation.
4. Use the formula: Use the formula x = -b/2a to find the axis of symmetry.

Applications of Axis of Symmetry

The axis of symmetry has numerous applications in various fields, including:

• Geometry: The axis of symmetry is used to create symmetrical patterns in geometry.
• Algebra: The axis of symmetry is used to graph functions in algebra.
• Physics: The axis of symmetry is used to describe the symmetry of physical systems.
• Engineering: The axis of symmetry is used to design symmetrical structures in engineering.

Real-World Examples of Axis of Symmetry

Here are a few real-world examples of axis of symmetry:

• Butterfly wings: The wings of a butterfly exhibit symmetry about the axis of symmetry, which runs down the center of the wing.
• Skyscrapers: Many skyscrapers exhibit symmetry about the axis of symmetry, which runs down the center of the building.
• Bridges: Some bridges exhibit symmetry about the axis of symmetry, which runs down the center of the bridge.

Conclusion

In conclusion, the axis of symmetry is a fundamental concept in mathematics that helps in understanding the properties of various geometric shapes and functions. By understanding the axis of symmetry, we can create symmetrical patterns, graph functions, and describe the symmetry of physical systems.

Whether you are a student, a teacher, or simply someone who loves mathematics, understanding the axis of symmetry can make a significant difference in how you perceive and interact with the world. So, the next time you see a butterfly wing or a skyscraper, remember the axis of symmetry that makes them symmetrical.

Now that you've reached the end of this article, we invite you to share your thoughts on the axis of symmetry. Have you encountered any real-world examples of axis of symmetry? Share your experiences in the comments below.