Convert 8.3e-6 To Standard Form Easily

Quick Links :

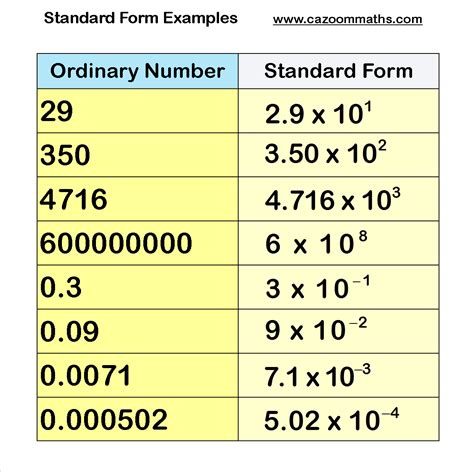
Understanding Standard Form

Standard form, also known as scientific notation, is a way of expressing very large or very small numbers in a more manageable form. It consists of a number between 1 and 10, multiplied by a power of 10. This notation is widely used in mathematics, physics, and engineering to simplify complex calculations and make them more readable.

The Importance of Standard Form

Standard form is essential in various fields, such as physics, chemistry, and mathematics, where calculations involve very large or very small numbers. It helps to:

• Simplify complex calculations
• Avoid errors caused by rounding or truncation
• Improve readability and clarity of mathematical expressions
• Facilitate comparison and analysis of large datasets

Converting 8.3e-6 to Standard Form

To convert 8.3e-6 to standard form, we need to follow these steps:

• Identify the coefficient (8.3) and the exponent (-6)
• Move the decimal point of the coefficient to the left by 6 places, as indicated by the exponent
• The resulting number is 0.0000083
• Express the number in standard form by multiplying it by 10 raised to the power of -6

Therefore, 8.3e-6 in standard form is 8.3 × 10^(-6).

Alternative Method

Alternatively, you can use the fact that 1e-6 is equal to 1 × 10^(-6). Therefore, 8.3e-6 can be rewritten as 8.3 × 1e-6 = 8.3 × 1 × 10^(-6) = 8.3 × 10^(-6).

Common Mistakes to Avoid

When converting numbers to standard form, it's essential to avoid common mistakes, such as:

• Moving the decimal point in the wrong direction
• Forgetting to adjust the exponent accordingly
• Rounding or truncating the coefficient

By avoiding these mistakes, you can ensure accurate and reliable results in your calculations.

Practice Exercises

To reinforce your understanding of standard form, try the following practice exercises:

• Convert 4.2e-3 to standard form
• Convert 9.5e-2 to standard form
• Convert 1.8e-4 to standard form

Check your answers with a calculator or by using the alternative method.

Real-World Applications of Standard Form

Standard form has numerous real-world applications, including:

• Physics and engineering: to describe very large or very small physical quantities, such as distances, velocities, and energies
• Chemistry: to express concentrations, reaction rates, and equilibrium constants
• Mathematics: to simplify complex calculations and improve readability of mathematical expressions

By understanding standard form and how to convert numbers to it, you can appreciate its significance and relevance in various fields.

We hope this article has helped you understand the concept of standard form and how to convert numbers to it. If you have any questions or need further clarification, please don't hesitate to ask. Share your thoughts and experiences with standard form in the comments section below.