Simplify 72 To Simplest Radical Form Explained

Quick Links :

Simplifying radicals is an essential concept in mathematics, particularly in algebra and geometry. It involves expressing a radical expression in its simplest form, making it easier to work with and understand. In this article, we will explore the concept of simplifying radicals, specifically the expression 72, and provide a step-by-step guide on how to simplify it.

What are Radicals?

A radical is a mathematical expression that contains a root symbol (√). It represents a number that, when raised to a power, gives a specified value. Radicals can be expressed in different forms, including square roots (√), cube roots (³√), and nth roots (ⁿ√).

Why Simplify Radicals?

Simplifying radicals is essential for several reasons:

1. Easier calculations: Simplifying radicals makes it easier to perform calculations, as it reduces the complexity of the expression.
2. Clearer understanding: Simplifying radicals helps to clarify the meaning of the expression, making it easier to understand and work with.
3. Improved accuracy: Simplifying radicals reduces the likelihood of errors, as it eliminates unnecessary complexity.

Simplifying 72

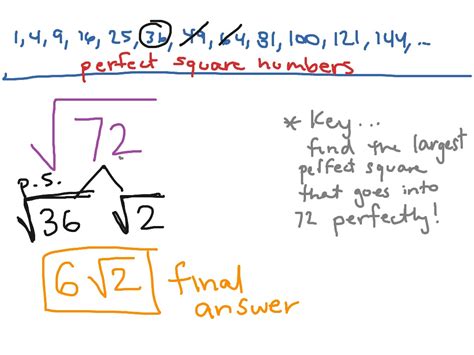
To simplify 72, we need to find the largest perfect square that divides 72. A perfect square is a number that can be expressed as the square of an integer. For example, 4, 9, and 16 are perfect squares.

Here's a step-by-step guide on how to simplify 72:

Step 1: Factorize 72

First, we need to factorize 72 into its prime factors. The prime factorization of 72 is:

72 = 2 × 2 × 2 × 3 × 3

Step 2: Identify Perfect Squares

Next, we need to identify the perfect squares in the prime factorization of 72. We can see that 2 × 2 = 4, which is a perfect square, and 3 × 3 = 9, which is also a perfect square.

Step 3: Simplify the Radical

Now, we can simplify the radical by expressing it in terms of the perfect squares we identified:

72 = √(2 × 2 × 2 × 3 × 3) = √(4 × 9 × 2) = √(4) × √(9) × √(2) = 2 × 3 × √(2) = 6√(2)

Therefore, the simplest radical form of 72 is 6√(2).

Tips and Tricks

Here are some tips and tricks to help you simplify radicals:

1. Look for perfect squares: Always look for perfect squares in the prime factorization of the number.
2. Use the square root property: If you have a perfect square inside the radical, you can simplify it using the square root property.
3. Simplify before multiplying: Always simplify the radical before multiplying or dividing.

Conclusion

Simplifying radicals is an essential skill in mathematics, and it's not as complicated as it seems. By following the steps outlined in this article, you can simplify radicals with ease. Remember to look for perfect squares, use the square root property, and simplify before multiplying. With practice and patience, you'll become a pro at simplifying radicals in no time!

What's Next?

Now that you've learned how to simplify radicals, it's time to practice. Try simplifying other radical expressions, such as 48, 75, or 120. You can also explore other mathematical concepts, such as algebra and geometry, to deepen your understanding of radicals.

Get Involved

We'd love to hear from you! Share your thoughts, questions, and experiences with simplifying radicals in the comments below. Don't forget to like and share this article with your friends and family who might find it helpful.