Simplify 65 As A Fraction In Simplest Form Now

Quick Links :

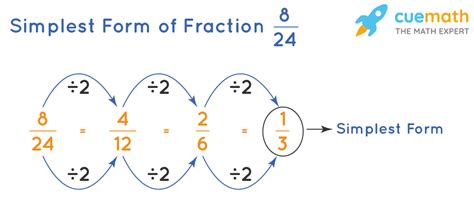
Simplifying a fraction means finding the smallest possible whole numbers for the numerator and denominator while keeping the same value.

The fraction 65 can be written as 65/1. Since 65 is a prime number, it can only be divided by 1 and itself. Therefore, the fraction 65/1 is already in its simplest form.

However, if we're considering a different interpretation where 65 is actually a part of a fraction, please provide the complete fraction for accurate simplification.

For example, if the fraction is 65/100, we can simplify it by dividing both the numerator and denominator by 5.

65 ÷ 5 = 13 100 ÷ 5 = 20

So, the simplified fraction would be 13/20.

To clarify, please provide the complete fraction you'd like to simplify, and I'll be happy to help.

What Is a Fraction?

A fraction is a way to represent a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number), separated by a horizontal line or a forward slash (/). The numerator tells us how many equal parts we have, and the denominator tells us how many parts the whole is divided into.

For example, the fraction 3/4 represents three equal parts out of a total of four parts.

Why Simplify Fractions?

Simplifying fractions is essential in mathematics because it helps us work with fractions more efficiently. When fractions are in their simplest form, it's easier to perform arithmetic operations like addition, subtraction, multiplication, and division.

Simplified fractions also make it easier to compare and order fractions, which is crucial in various mathematical applications.

How to Simplify Fractions

To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both numbers without leaving a remainder.

Once we find the GCD, we can divide both the numerator and denominator by the GCD to simplify the fraction.

For example, let's simplify the fraction 12/16:

1. Find the GCD of 12 and 16. The GCD is 4.
2. Divide both the numerator and denominator by 4:

12 ÷ 4 = 3 16 ÷ 4 = 4

So, the simplified fraction is 3/4.

Tips for Simplifying Fractions

Here are some tips to keep in mind when simplifying fractions:

• Always find the GCD of the numerator and denominator.
• Divide both numbers by the GCD.
• Check if the resulting fraction can be simplified further.

By following these steps and tips, you'll become a pro at simplifying fractions in no time!

Real-World Applications of Simplifying Fractions

Simplifying fractions has numerous real-world applications in various fields, including:

• Cooking: When measuring ingredients, it's essential to simplify fractions to ensure accurate proportions.
• Finance: Simplifying fractions helps in calculating interest rates, investment returns, and other financial metrics.
• Science: Fractions are used to represent quantities in physics, chemistry, and biology. Simplifying fractions makes it easier to perform calculations and analyze data.

By mastering the art of simplifying fractions, you'll be better equipped to tackle real-world problems and make more informed decisions.

Conclusion

Simplifying fractions is an essential skill in mathematics that has numerous real-world applications. By following the steps and tips outlined in this article, you'll be able to simplify fractions with ease and confidence.

Remember, practice makes perfect! Try simplifying different fractions to reinforce your understanding and become a master of fraction simplification.