4.035 In Expanded Form: Simplifying The Decimal

Quick Links :

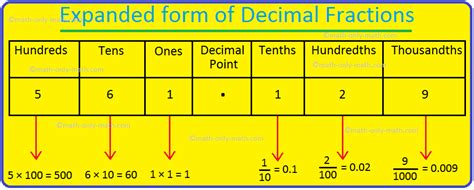
The concept of expanded form in mathematics is a fundamental idea that helps us understand the value of numbers, especially decimals. In this article, we will delve into the world of expanded form, focusing specifically on the number 4.035. We will break down what it means, how it works, and why it's essential in various mathematical operations.

Understanding Expanded Form

Expanded form is a way of expressing numbers in a more detailed manner, showing the value of each digit. It's like breaking down a number into its constituent parts, allowing us to see the individual contributions of each digit to the overall value. This concept is crucial in mathematics, as it helps us perform calculations, understand place value, and develop a deeper understanding of numerical relationships.

What is Expanded Form in Decimals?

When dealing with decimals, expanded form becomes even more critical. Decimals are a way of expressing fractions in a more compact form, but they can be tricky to work with, especially when performing operations like addition, subtraction, multiplication, and division. Expanded form helps us navigate these challenges by breaking down decimals into their individual parts.

The Number 4.035 in Expanded Form

Now, let's take a closer look at the number 4.035 in expanded form. To do this, we'll break down the number into its individual parts, showing the value of each digit.

4.035 = 4 + 0.03 + 0.0005

As we can see, the number 4.035 can be expressed as the sum of three parts:

• 4 (the whole number part)
• 0.03 (the tenths part)
• 0.0005 (the thousandths part)

This expanded form representation helps us understand the individual contributions of each digit to the overall value of the number.

Working with Expanded Form in Decimals

Now that we've seen how to express 4.035 in expanded form, let's explore how this representation can help us perform mathematical operations.

Addition and Subtraction

When adding or subtracting decimals, it's essential to line up the decimal points correctly. Expanded form can help us do this by breaking down the numbers into their individual parts.

For example, let's say we want to add 4.035 and 2.017. We can express both numbers in expanded form and then add the corresponding parts:

4.035 = 4 + 0.03 + 0.0005 2.017 = 2 + 0.01 + 0.0007

Now, we can add the corresponding parts:

4 + 2 = 6 0.03 + 0.01 = 0.04 0.0005 + 0.0007 = 0.0012

So, the sum is:

6 + 0.04 + 0.0012 = 6.0412

Multiplication and Division

Expanded form can also help us with multiplication and division operations. When multiplying decimals, we need to multiply the corresponding parts and then combine the results.

For example, let's say we want to multiply 4.035 by 3. We can express both numbers in expanded form and then multiply the corresponding parts:

4.035 = 4 + 0.03 + 0.0005 3 = 3 + 0 + 0

Now, we can multiply the corresponding parts:

4 × 3 = 12 0.03 × 3 = 0.09 0.0005 × 3 = 0.0015

So, the product is:

12 + 0.09 + 0.0015 = 12.0915

When dividing decimals, we need to divide the corresponding parts and then combine the results.

For example, let's say we want to divide 4.035 by 2. We can express both numbers in expanded form and then divide the corresponding parts:

4.035 = 4 + 0.03 + 0.0005 2 = 2 + 0 + 0

Now, we can divide the corresponding parts:

4 ÷ 2 = 2 0.03 ÷ 2 = 0.015 0.0005 ÷ 2 = 0.00025

So, the quotient is:

2 + 0.015 + 0.00025 = 2.01525

Benefits of Using Expanded Form in Decimals

Using expanded form in decimals has several benefits, including:

• Improved understanding: Expanded form helps us understand the individual contributions of each digit to the overall value of the number.
• Easier calculations: By breaking down decimals into their individual parts, we can perform calculations more easily and accurately.
• Better estimation: Expanded form allows us to estimate calculations more accurately, which is essential in real-world applications.
• Develops problem-solving skills: Working with expanded form in decimals helps us develop problem-solving skills, as we need to think critically about the relationships between numbers.

Real-World Applications of Expanded Form in Decimals

Expanded form in decimals has numerous real-world applications, including:

• Science and engineering: Expanded form is essential in scientific and engineering calculations, where accuracy and precision are critical.
• Finance and economics: Expanded form is used in financial calculations, such as interest rates and investment returns.
• Medicine and health: Expanded form is used in medical calculations, such as dosages and treatment plans.
• Computer programming: Expanded form is used in programming, where accuracy and precision are essential.

Conclusion

Expanded form in decimals is a powerful tool that helps us understand and work with decimals more effectively. By breaking down decimals into their individual parts, we can perform calculations more easily and accurately, develop problem-solving skills, and estimate calculations more accurately. Whether you're a student, teacher, or professional, understanding expanded form in decimals is essential for success in mathematics and real-world applications.

We hope this article has helped you understand the concept of expanded form in decimals and its significance in mathematics and real-world applications. If you have any questions or comments, please feel free to share them below.