Add 2 Fractions In 5 Easy Steps

Quick Links :

Adding fractions is a fundamental math concept that can seem daunting at first, but with the right approach, it can be done with ease. In this article, we will break down the process of adding fractions into 5 easy steps, making it accessible to readers of all ages and skill levels.

Why Adding Fractions is Important

Fractions are a crucial part of mathematics, and being able to add them is essential for solving various mathematical problems. From simple calculations to complex algebraic equations, adding fractions is a fundamental skill that can benefit individuals in various aspects of life, including science, engineering, economics, and even cooking. By mastering the art of adding fractions, you can develop problem-solving skills, critical thinking, and analytical abilities that can be applied to real-world situations.

Common Challenges in Adding Fractions

One of the most common challenges people face when adding fractions is dealing with different denominators. When fractions have different denominators, it can be tricky to find a common ground to add them. However, with the right approach, this challenge can be overcome. Another challenge is ensuring that the fractions are simplified correctly after addition.

5 Easy Steps to Add 2 Fractions

Step 1: Identify the Denominators

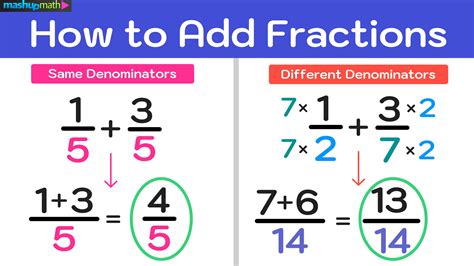
The first step in adding fractions is to identify the denominators of both fractions. The denominator is the number at the bottom of the fraction. For example, in the fraction 1/2, the denominator is 2. Once you have identified the denominators, you can proceed to the next step.

Step 2: Find the Least Common Multiple (LCM)

What is the Least Common Multiple (LCM)?

The Least Common Multiple (LCM) is the smallest number that is a multiple of both denominators. To find the LCM, you can list the multiples of each denominator and find the smallest number that appears in both lists. For example, if the denominators are 4 and 6, the multiples of 4 are 4, 8, 12, 16, and so on, while the multiples of 6 are 6, 12, 18, and so on. The smallest number that appears in both lists is 12, which is the LCM.

Step 3: Convert the Fractions to Have the LCM as the Denominator

Once you have found the LCM, you can convert both fractions to have the LCM as the denominator. To do this, you need to multiply the numerator and denominator of each fraction by the necessary number to get the LCM as the denominator. For example, if the fractions are 1/4 and 1/6, and the LCM is 12, you can convert the fractions as follows:

• 1/4 = (1 x 3) / (4 x 3) = 3/12
• 1/6 = (1 x 2) / (6 x 2) = 2/12

Step 4: Add the Fractions

Adding the Fractions

Now that both fractions have the same denominator (LCM), you can add them by adding the numerators. For example, if the fractions are 3/12 and 2/12, you can add them as follows:

• 3/12 + 2/12 = (3 + 2) / 12 = 5/12

Step 5: Simplify the Result (Optional)

If the result is not in its simplest form, you can simplify it by dividing both the numerator and denominator by their greatest common divisor (GCD). For example, if the result is 5/12, and the GCD of 5 and 12 is 1, then the result is already in its simplest form. However, if the result is 6/12, you can simplify it as follows:

• 6/12 = (6 ÷ 2) / (12 ÷ 2) = 3/6

And that's it! With these 5 easy steps, you can add 2 fractions with ease.

Conclusion: Take Action and Practice

Adding fractions is a fundamental math concept that can be mastered with practice and patience. By following the 5 easy steps outlined in this article, you can become proficient in adding fractions and develop problem-solving skills that can benefit you in various aspects of life. Take action today and start practicing adding fractions. Share your thoughts and feedback in the comments below, and don't forget to share this article with your friends and family who may benefit from it.